题目内容
德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数 被称为狄利克雷函数,其中
被称为狄利克雷函数,其中 为实数集,
为实数集,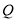 为有理数集,则关于函数
为有理数集,则关于函数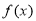 有如下四个结论:
有如下四个结论:
①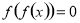 ; ②函数
; ②函数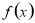 是偶函数; ③任取一个不为零的有理数
是偶函数; ③任取一个不为零的有理数 对任意的
对任意的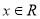 恒成立; ④存在三个点
恒成立; ④存在三个点 ,使得
,使得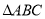 为等边三角形.
为等边三角形.
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
C
【解析】
试题分析:由题意知, ,故
,故 ,故①是假命题;
,故①是假命题;
当 时,
时, ,则
,则 ;当
;当 时,
时, ,则
,则 ,故函数
,故函数 是偶函数,②是真命题;
是偶函数,②是真命题;
任取一个不为零的有理数 ,若
,若 ,则
,则 是有理数;若
是有理数;若 ,则
,则 ,∴都有
,∴都有 ,故③是真命题;
,故③是真命题;
取点 ,
, ,
, 是等边三角形,故④是真命题.
是等边三角形,故④是真命题.
故答案为C.
考点:函数的性质

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
 的焦点到它的准线的距离等于 .
的焦点到它的准线的距离等于 . ( )
( ) B.
B. C.
C. D.
D.
 = .
= .
 ,则
,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 ,PA
,PA 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC=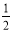 AB=1,M是PB的中点。
AB=1,M是PB的中点。
 面PCD;
面PCD;
 B.
B.
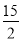 D.
D.