题目内容
(14分)设函数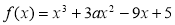 ,若
,若 在
在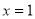 处有极值
处有极值
(1)求实数 的值
的值
(2)求函数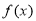 的极值
的极值
(3)若对任意的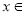
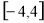 ,都有
,都有 ,求实数
,求实数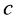 的取值范围
的取值范围
(1)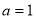 ;(2),极大值
;(2),极大值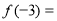 32, 极小值
32, 极小值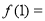 0; (3)
0; (3)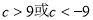 .
.
【解析】
试题分析:(1)先求导,由题意可知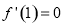 ,则可得
,则可得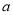 的值. (2)讨论导数的正负,导数正得函数的增区间,导数负得函数的减区间.根据函数的单调性可求得极值. (3)可将问题转化为函数
的值. (2)讨论导数的正负,导数正得函数的增区间,导数负得函数的减区间.根据函数的单调性可求得极值. (3)可将问题转化为函数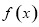 的最大值交于
的最大值交于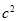 ,由(2)可求得函数
,由(2)可求得函数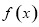 在
在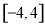 上的最大值.
上的最大值.
试题解析:【解析】
(1)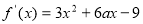 ,由已知得
,由已知得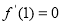 ,解得
,解得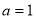 ..3分
..3分
(2)由(1)得: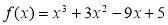 ,则
,则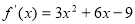
令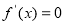 ,解得
,解得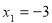 ,
,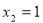 ..5分
..5分
当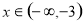 ,
,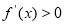 ,当
,当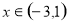 ,
,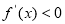 ,当
,当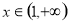 ,
,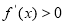
所以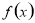 在
在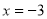 处取得极大值,极大值
处取得极大值,极大值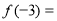 32
32
在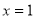 处取得极小值,极小值
处取得极小值,极小值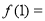 0 ..9分
0 ..9分
(3)由(2)可知极大值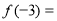 32,极小值
32,极小值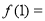 0
0
又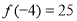 ,
,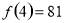 ,所以函数
,所以函数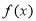 在
在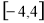 上的最大值为81 11分
上的最大值为81 11分
对任意的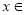
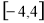 ,都有
,都有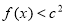 ,则
,则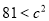 ,解得
,解得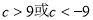 14分
14分
考点:用导数研究函数的性质.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
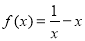 的图像关于( )
的图像关于( )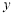 轴对称 B. 直线
轴对称 B. 直线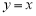 对称 C. 坐标原点对称 D. 直线
对称 C. 坐标原点对称 D. 直线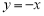 对称
对称 与圆
与圆 相交于A、B两点,则AB的长度等于
相交于A、B两点,则AB的长度等于 C.
C. D.
D.
 的焦点到它的准线的距离等于 .
的焦点到它的准线的距离等于 . 的离心率
的离心率
 B.
B. C.
C. D.
D.
 中,已知
中,已知 ,则
,则 __________
__________ 共焦点且过点
共焦点且过点 的双曲线方程是( )
的双曲线方程是( ) B.
B. C.
C. D.
D.
 ,PA
,PA 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC=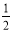 AB=1,M是PB的中点。
AB=1,M是PB的中点。
 面PCD;
面PCD;