题目内容
6.已知数列{an}满足:a1=$\frac{1}{4}$,an=$\frac{{{a_{n-1}}}}{{{{({-1})}^n}{a_{n-1}}-2}}$(n≥2,n∈N*),设bn=$\frac{1}{a_n}+{({-1})^n}$.(1)求证:数列{bn}是等比数列,并求数列{an}的通项公式;
(2)求数列$\left\{{\frac{3n-2}{b_n}}\right\}$的前n项和Sn.
分析 (1)通过代入化简可知bn=-2bn-1(n≥2 ),然后验证当n=1是否成立,进而计算可得结论;
(2)通过(1)可知$\frac{3n-2}{b_n}=\frac{3n-2}{{3×{{({-2})}^{n-1}}}}$,进而利用错位相减法计算即得结论.
解答 (1)证明:由${a_1}=\frac{1}{4}$,${a_n}=\frac{{{a_{n-1}}}}{{{{({-1})}^n}{a_{n-1}}-2}}$ (n≥2,n∈N* ),得:
$\frac{1}{a_n}+{({-1})^n}=-2[{\frac{1}{{{a_{n-1}}}}+{{({-1})}^{n-1}}}]$,
所以bn=-2bn-1 (n≥2 ),
又${b_1}=\frac{1}{a_1}+{({-1})^1}=3≠0$,
所以$\frac{b_n}{{{b_{n-1}}}}=-2$ (n≥2 ),
所以数列{bn} 是等比数列,${b_n}=3×{({-2})^{n-1}}$ (n≥2 ),
又∵b1=3,
∴${b_n}=3×{({-2})^{n-1}}$ (n∈N* ),${a_n}=\frac{1}{{3×{{({-2})}^{n-1}}+{{({-1})}^{n-1}}}}$ (n∈N* );
(2)解:由(1)可知$\frac{3n-2}{b_n}=\frac{3n-2}{{3×{{({-2})}^{n-1}}}}$,
∴${S_n}=\frac{1}{{3×{{({-2})}^0}}}+\frac{4}{{3×{{({-2})}^1}}}+\frac{7}{{3×{{({-2})}^2}}}+…+\frac{3n-2}{{3×{{({-2})}^{n-1}}}}$,
$-\frac{1}{2}{S_n}=\frac{1}{{3×{{({-2})}^1}}}+\frac{4}{{3×{{({-2})}^2}}}+\frac{7}{{3×{{({-2})}^3}}}+…+\frac{3n-5}{{3×{{({-2})}^{n-1}}}}+\frac{3n-2}{{3×{{({-2})}^n}}}$,
两式相减,$\frac{3}{2}{S_n}=\frac{1}{3}+\frac{1}{{{{({-2})}^1}}}+\frac{1}{{{{({-2})}^2}}}+\frac{1}{{{{({-2})}^3}}}+…+\frac{1}{{{{({-2})}^{n-1}}}}-\frac{3n-2}{{3×{{({-2})}^n}}}=-n•{({-\frac{1}{2}})^n}$,
故${S_n}=\frac{n}{3}{({-\frac{1}{2}})^{n-1}}$.
点评 本题考查数列的通项及前n项和,考查错位相减法,注意解题方法的积累,属于中档题.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案| 上一年出险次数 | 0 | 1 | 2 | 3 | 4 | 5次以上(含5次) |
| 下一年保费倍率 | 85% | 100% | 125% | 150% | 175% | 200% |
| 连续两年没出险打7折,连续三年没出险打6折 | ||||||
(1)求b;
(2)广东李先生2016年1月购买一辆价值20万元的新车
①估计李先生购车时 的商业车险保费;
②若该车今年2月份已出过一次险,现在有被刮花了,李先生到汽车维修4S店询价,预计修车费用为800元,保险专家建议李先生自费(即不出险),你认为李先生是否应该接受建议?说明理由.(假设车辆下一年与上一年都购买相同的商业车险产品进行续保)

| A. | 7 | B. | 8 | C. | 10 | D. | 11 |
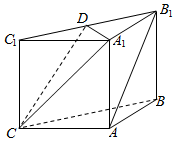 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,AB=AC=1,∠BAC=90,点D是棱B1C1的中点.
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,AB=AC=1,∠BAC=90,点D是棱B1C1的中点.