己知x.y为实数.代数式$\sqrt{1+(y-2)^{2}}$+$\sqrt{9+(3-x)^{2}}$+$\sqrt{{x}^{2}+{y}^{2}}$的最小值是$\sqrt{5}$+3$\sqrt{2}$．题目和参考答案——青夏教育精英家教网—

题目内容

18．己知x，y为实数，代数式$\sqrt{1+（y-2）^{2}}$+$\sqrt{9+（3-x）^{2}}$+$\sqrt{{x}^{2}+{y}^{2}}$的最小值是$\sqrt{5}$+3$\sqrt{2}$．

分析根据$\sqrt{1+（y-2）^{2}}$+$\sqrt{9+（3-x）^{2}}$+$\sqrt{{x}^{2}+{y}^{2}}$的几何意义结合图象求出最小值即可．

解答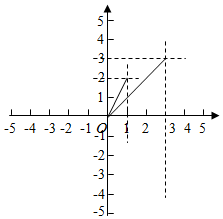解：$\sqrt{1+（y-2）^{2}}$的几何意义表示（0，y），（1，2）的距离，
$\sqrt{9+（3-x）^{2}}$的几何意义表示（x，0），（3，3）的距离，
$\sqrt{{x}^{2}+{y}^{2}}$的几何意义表示（x，y），（0，0）的距离，
如图示：
，
结合图象x=0，y=0时，
代数式$\sqrt{1+（y-2）^{2}}$+$\sqrt{9+（3-x）^{2}}$+$\sqrt{{x}^{2}+{y}^{2}}$的最小值是$\sqrt{5}$+3$\sqrt{2}$，
故答案为：$\sqrt{5}$+3$\sqrt{2}$．

点评本题考查了求函数的最值问题，考查数形结合思想，是一道中档题．

练习册系列答案

	A．	以4为首项，3为公比的等比数列		B．	以4为首项，$\frac{1}{3}$为公比的等比数列
	C．	以$\frac{4}{3}$为首项，3为公比的等比数列		D．	以$\frac{4}{3}$为首项，$\frac{1}{3}$为公比的等比数列

9．若函数f（x）=$\left\{\begin{array}{l}{{x}^{2}-3x+1，x≥1}\\{（\frac{1}{2}）^{x}+\frac{1}{2}，x＜1}\end{array}\right.$，则f（f（2））=（　　）

6．已知数列{a_n}满足：a₁=$\frac{1}{4}$，a_n=$\frac{{{a_{n-1}}}}{{{{（{-1}）}^n}{a_{n-1}}-2}}$（n≥2，n∈N^*），设b_n=$\frac{1}{a_n}+{（{-1}）^n}$．
（1）求证：数列{b_n}是等比数列，并求数列{a_n}的通项公式；
（2）求数列$\left\{{\frac{3n-2}{b_n}}\right\}$的前n项和S_n．

13．在△ABC中，角A，B，C所对的边分别为a，b，c，sinA，sinC，sinB成等比数列，且b=2a．
（1）求cosC的值；
（2）若△ABC的面积为2$\sqrt{7}$sinAsinB，求sinA及c的值．

3．某种商品价格与该商品日需求量之间的几组对照数据如表：