题目内容
若直线y=x+m与曲线x=
只有一个公共点,则实数m的取值范围是( )
| 1-y2 |
A、m=±
| ||||
B、m≥
| ||||
C、-
| ||||
D、-1<m≤1或m=-
|
考点:直线与圆相交的性质
专题:直线与圆
分析:由x=
,化简得x2+y2=1,注意到x≥0,所以这个曲线应该是半径为1,圆心是(0,0)的半圆,且其图象只在一、四象限.画出图象,这样因为直线与其只有一个交点,由此能求出实数m的取值范围.
| 1-y2 |
解答:
解:由x=
,化简得x2+y2=1,注意到x≥0,
所以这个曲线应该是半径为1,圆心是(0,0)的半圆,
且其图象只在一、四象限.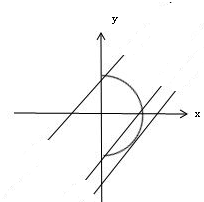
画出图象,这样因为直线与其只有一个交点,
从图上看出其三个极端情况分别是:
①直线在第四象限与曲线相切,
②交曲线于(0,-1)和另一个点,
③与曲线交于点(0,1).
直线在第四象限与曲线相切时解得m=-
,
当直线y=x+m经过点(0,1)时,m=1.
当直线y=x+m经过点(0,-1)时,m=-1,所以此时-1<m≤1.
综上满足只有一个公共点的实数m的取值范围是:
-1<m≤1或m=-
.
故选:D.
| 1-y2 |
所以这个曲线应该是半径为1,圆心是(0,0)的半圆,
且其图象只在一、四象限.

画出图象,这样因为直线与其只有一个交点,
从图上看出其三个极端情况分别是:
①直线在第四象限与曲线相切,
②交曲线于(0,-1)和另一个点,
③与曲线交于点(0,1).
直线在第四象限与曲线相切时解得m=-
| 2 |
当直线y=x+m经过点(0,1)时,m=1.
当直线y=x+m经过点(0,-1)时,m=-1,所以此时-1<m≤1.
综上满足只有一个公共点的实数m的取值范围是:
-1<m≤1或m=-
| 2 |
故选:D.
点评:本题考查实数的取值范围的求法,是中档题,解题时要认真审题,注意数形结合思想的合理运用.

练习册系列答案
相关题目
定义在R上的函数f(x)满足(x+2)•f′(x)<0(其中f′(x)是函数f(x)的导数),又a=f(log23),b=f(1),c=f(ln3),则( )
| A、a<c<b |
| B、b<c<a |
| C、c<a<b |
| D、c<b<a |
对于定义域为D的函数y=f(x)和常数c,若对任意正实数ξ,?x∈D,使得0<|f(x)-c|<ξ恒成立,则称函数y=f(x)为“敛c函数”,现给出如下函数:
①f(x)=x(x∈Z);
②f(x)=(
)x+2(x∈Z);
③f(x)=log2x+1;
④f(x)=
.
其中为“敛2函数”的有( )
①f(x)=x(x∈Z);
②f(x)=(
| 1 |
| 2 |
③f(x)=log2x+1;
④f(x)=
| 2x-1 |
| 2x |
其中为“敛2函数”的有( )
| A、①② | B、③④ |
| C、①②③ | D、②③④ |
直线y=x-4与抛物线y2=2x所围成的图形面积是( )
| A、15 | B、16 | C、17 | D、18 |
已知函数f(x)=
sinωx+cosωx(ω>0)的图象与直线y=-2的两个相邻公共点之间的距离等于π,则f(x)的单调递减区间是( )
| 3 |
A、[kπ+
| ||||
B、[kπ-
| ||||
C、[2kπ+
| ||||
D、[2kπ-
|
已知a+2b=2(a,b>0),则ab的最大值为( )
A、
| ||
| B、2 | ||
| C、3 | ||
D、
|
平面直角坐标系中,由不等式组
围成的区域的面积是( )
|
| A、6 | B、7 | C、8 | D、9 |