题目内容
1.已知a,b,c分别为△ABC三个内角A,B,C的对边,acosC+$\sqrt{3}$asinC-b-2c=0.(1)求A.
(2)若等差数列{an}的公差不为零,且a1cosA=-1,且a2、a4、a8成等比数列,设{an}的前n项和为Tn,求数列{$\frac{1}{{T}_{n}}$}的前n项和Sn.
分析 (1)利用正弦定理对acosC+$\sqrt{3}$asinC-b-2c=0变形、结合三角形内角和定理可知$\sqrt{3}$sinA-cosA=2,进而利用辅助角公式可得结论;
(2)通过(1)可知a1=2,利用a2、a4、a8成等比数列可知数列{an}是首项、公差均为2的等差数列,利用等差数列的求和公式可知Tn=n(n+1),进而利用裂项相消法计算即得结论.
解答 解:(1)因为acosC+$\sqrt{3}$asinC-b-2c=0,
所以sinAcosC+$\sqrt{3}$sinAsinC-sinB-2sinC=0,
所以sinAcosC+$\sqrt{3}$sinAsinC=sinB+2sinC=sin(A+C)+2sinC=sinAcosC+sinCcosA+2sinC,
又因为sinC≠0,
所以$\sqrt{3}$sinA-cosA=2,
∴sin(A-30°)=1,
∴A-30°=90°,
∴A=120°;
(2)由(1)可知cosA=cos120°=-$\frac{1}{2}$,
又因为a1cosA=-1,
所以a1=2,记等差数列{an}的公差为d(d≠0),
则由a2、a4、a8成等比数列可知(2+3d)2=(2+d)(2+7d),解得:d=2,
所以数列{an}是首项、公差均为2的等差数列,
所以数列{an}的前n项和Tn=2×$\frac{n(n+1)}{2}$=n(n+1),
因为$\frac{1}{{T}_{n}}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,
所以Sn=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$.
点评 本题考查三角恒等变换,考查数列的通项及前n项和,考查正弦定理、辅助角公式,考查裂项相消法,考查运算求解能力,注意解题方法的积累,属于中档题.

| 最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
| 天数 | 2 | 16 | 36 | 25 | 7 | 4 |
(1)求六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
| A. | (-1,2) | B. | (0,1) | C. | (-1,0) | D. | (1,2) |
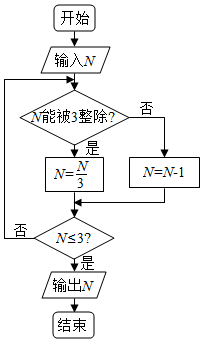 阅读右面的程序框图,运行相应的程序,若输入N的值为24,则输出N的值为( )
阅读右面的程序框图,运行相应的程序,若输入N的值为24,则输出N的值为( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |