题目内容

19．已知函数$f（x）=\left\{{\begin{array}{l}{{x^2}-x}\\{x+1}\end{array}}\right.，\begin{array}{l}{（x≥0）}\\{（x＜0）}\end{array}$，则f（2）=2．

分析 根据分段函数的表达式，直接代入即可．

解答 解：由分段函数的表达式得f（2）=22-2=4-2=2，
故答案为：2

点评 本题主要考查函数值的计算，根据分段函数的表达式利用代入法是解决本题的关键．比较基础．

练习册系列答案
相关题目
11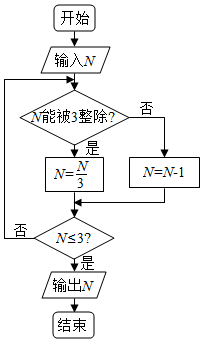．阅读右面的程序框图，运行相应的程序，若输入N的值为24，则输出N的值为（　　）
A．0B．1C．2D．3
10．已知X的概率分布为
 X-1 0 1 2
 Pk $\frac{1}{8}$ $\frac{1}{8}$ $\frac{1}{4}$$\frac{1}{2}$
求Y1=2X-1与Y2=X2的分布列．
7．某公司的组织结构图如图所示，则开发部的直接领导是总经理．
14．已知函数f（x）=$\left\{\begin{array}{l}{（\frac{1}{2}）^{x}，x＜0}\\{x-2，x≥0}\end{array}\right.$，若f[f（-2）]=a，实数x，y满足约束条件$\left\{\begin{array}{l}{x-a≥0}\\{x+y≤6}\\{2x-y≤6}\end{array}\right.$，则目标函数z=$\frac{3x+4y+10}{x+2}$的最大值为8．
4．已知函数f（x）=$\frac{lnx}{x}$，g（x）=$\frac{m}{x}$+$\frac{1}{2}$（m∈R）．
（Ⅰ）当m=1时，求曲线y=g（x）在x=1处的切线方程；
（Ⅱ）求f（x）的单调区间并比较2017${\;}^{\frac{1}{2017}}$与2016${\;}^{\frac{1}{2016}}$的大小；
（Ⅲ）若对于任意正实数b，关于x的不等式bf（x）＞g（x）在区间[1，e]上恒成立，求实数m的取值范围．（其中e=2.71828…）
11．阅读下列伪代码，当a，b的输入值分别为2，3时，则输出的实数m的值是3．
8．设计院拟从4个国家级课题和6个省级课题中各选2个课题作为本年度的研究项目，若国家级课题A和省级课题B至少有一个被选中的不同选法种数是m，那么二项式（1+mx2）8的展开式中x4的系数为（　　）
A．54000B．100400C．100600D．100800
9．已知函数$f（x）=\left\{{\begin{array}{l}{{2^{1-x}}，x≤1}\\{1-log_2^x，x＞1}\end{array}}\right.$，则满足f（x）≤4的x取值范围是（　　）
A．[-1，+∞）B．$[\frac{1}{8}，+∞）$C．$[-1，\frac{1}{8}]$D．$[\frac{1}{8}，1]$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网