题目内容
19.若$\vec a$与$\vec b$满足$|{\vec a}|=8$,$|{\vec b}|=12$,则$|{\vec a+\vec b}|$的最小值为4.分析 设$\vec a$与$\vec b$的夹角为θ,θ∈[0,π];利用|$\overrightarrow{b}$|-|$\overrightarrow{a}$|≤|$\overrightarrow{a}$+$\overrightarrow{b}$|≤|$\overrightarrow{a}$|+|$\overrightarrow{b}$|,
得出θ=π时$|{\vec a+\vec b}|$取得最小值.
解答 解:设$\vec a$与$\vec b$的夹角为θ,则θ∈[0,π];
∵$|{\vec a}|=8$,$|{\vec b}|=12$,
∴|$\overrightarrow{b}$|-|$\overrightarrow{a}$|≤|$\overrightarrow{a}$+$\overrightarrow{b}$|≤|$\overrightarrow{a}$|+|$\overrightarrow{b}$|,
即4≤|$\overrightarrow{a}$+$\overrightarrow{b}$|≤20;
∴θ=π时,$|{\vec a+\vec b}|$取得最小值为4.
故答案为:4.
点评 本题考查了平面向量数量积中模长公式的应用问题,是基础题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
10.如图,输入n=5时,则输出的S=( )
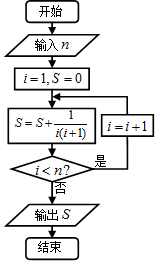

| A. | $\frac{3}{4}$ | B. | $\frac{4}{5}$ | C. | $\frac{5}{6}$ | D. | $\frac{6}{7}$ |
7.已知f(x)=${log}_{2}|x|{+3}^{|x|}$,则f(x2-1)<3的解集为( )
| A. | (-$\sqrt{2}$,-1)∪(-1,0)∪(0,1)∪(1,$\sqrt{2}$) | B. | (-$\sqrt{2}$,0)∪(0,$\sqrt{2}$) | ||
| C. | (-$\sqrt{2}$,$\sqrt{2}$) | D. | (-$\sqrt{2}$,-1)∪(1,$\sqrt{2}$) |
9.如图所示某公司的组织结构图,信息部被( )直接领导


| A. | 专家办公室 | B. | 开发部 | C. | 总工程师 | D. | 总经理 |