题目内容
13.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左,右焦点为F1,F2,离心率为e.P是椭圆上一点,满足PF2⊥F1F2,点Q在线段PF1上,且$\overrightarrow{{F_1}Q}=2\overrightarrow{QP}$.若$\overrightarrow{{F_1}P}•\overrightarrow{{F_2}Q}$=0,则e2=( )| A. | $\sqrt{2}-1$ | B. | $2-\sqrt{2}$ | C. | $2-\sqrt{3}$ | D. | $\sqrt{5}-2$ |
分析 由题意求得P点坐标,根据向量的坐标运算求得Q点坐标,由$\overrightarrow{{F_1}P}•\overrightarrow{{F_2}Q}$=0,求得b4=2c2a2,则b2=a2-c2,根据离心率的取值范围,即可求得椭圆的离心率.
解答 解:由题意可知:PF2⊥F1F2,则P(c,$\frac{{b}^{2}}{a}$),
由$\overrightarrow{{F_1}Q}=2\overrightarrow{QP}$,(xQ+c,yQ)=2(c-xQ,$\frac{{b}^{2}}{a}$-yQ),则Q($\frac{c}{3}$,$\frac{2{b}^{2}}{3a}$),
$\overrightarrow{{F}_{1}P}$=(2c,$\frac{{b}^{2}}{a}$),$\overrightarrow{{F}_{2}Q}$=(-$\frac{2c}{3}$,$\frac{2{b}^{2}}{3a}$),
由$\overrightarrow{{F_1}P}•\overrightarrow{{F_2}Q}$=0,则2c×(-$\frac{2c}{3}$)+$\frac{{b}^{2}}{a}$×$\frac{2{b}^{2}}{3a}$=0,整理得:b4=2c2a2,
则(a2-c2)2=2c2a2,整理得:a4-4c2a2+c4=0,则e4-4e2+1=0,解得:e2=2±$\sqrt{3}$,
由0<e<1,则e2=2-$\sqrt{3}$,
故选C.
点评 本题考查椭圆的离心率的求法,考查向量数量积的坐标运算,考查计算能力,属于中档题.

练习册系列答案
相关题目
4.在△ABC中,AC=2AB=2,∠BAC=120°,O是BC的中点,M是AO上一点,且$\overrightarrow{AO}$=3$\overrightarrow{MO}$,则$\overrightarrow{MB}$$•\overrightarrow{MC}$的值是( )
| A. | -$\frac{5}{3}$ | B. | -$\frac{7}{6}$ | C. | -$\frac{7}{3}$ | D. | -$\frac{5}{6}$ |
1.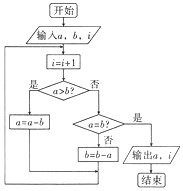 图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b,i的值分别为8,10,0,则输出的a和i和值分别为( )
图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b,i的值分别为8,10,0,则输出的a和i和值分别为( )
 图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b,i的值分别为8,10,0,则输出的a和i和值分别为( )
图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b,i的值分别为8,10,0,则输出的a和i和值分别为( )| A. | 2,5 | B. | 2,4 | C. | 0,4 | D. | 0,5 |
8.已知i为虚数单位,则$\frac{1+i}{3-i}$=( )
| A. | $\frac{2-i}{5}$ | B. | $\frac{2+i}{5}$ | C. | $\frac{1-2i}{5}$ | D. | $\frac{1+2i}{5}$ |
16.已知实数x,y满足$\left\{\begin{array}{l}{x+2y≥0}\\{x-y≤0}\\{0≤y≤k}\end{array}\right.$,且z=x+y的最大值为6,则(x+5)2+y2的最小值为( )
| A. | 5 | B. | 3 | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
17.已知点P是曲线C:xy=1(x>0)上的点,Q是点P关于直线l:y=2x的对称点,R为直线l与曲线C的交点,则$\overrightarrow{OR}$•$\overrightarrow{OQ}$的最小值为( )
| A. | $\sqrt{3}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |