题目内容
在平面直角坐标系xOy中，直线l过点（3，
）且倾斜角为
，在极坐标系（与直角坐标系xOy取相同的长度单位，且以原点O为极点，x轴的正半轴为极轴）中，圆C的方程为p=2
sinθ．
（1）求直线l的参数方程及圆C的直角坐标方程；
（2）设圆C与直线l交于A，B两点，若点P的坐标为（3，
），求|PA|•|PB|．
| 5 |
| π |
| 4 |
| 5 |
（1）求直线l的参数方程及圆C的直角坐标方程；
（2）设圆C与直线l交于A，B两点，若点P的坐标为（3，
| 5 |
考点：直线和圆的方程的应用
专题：综合题,直线与圆
分析：（1）利用直线l过点（3，
）且倾斜角为
，可得参数方程；根据x=ρcosθ、y=ρsinθ可得圆C的直角坐标方程；
（2）利用参数的几何意义，即可求|PA|•|PB|．
| 5 |
| π |
| 4 |
（2）利用参数的几何意义，即可求|PA|•|PB|．
解答：
解：（1）直线l过点（3，
）且倾斜角为
，参数方程为
（t为参数）；
圆C的方程为p=2
sinθ，直角坐标方程为x2+（y-
）2=5；
（2）
（t为参数），代入x2+（y-
）2=5，可得t2+3
t+4=0，
∵点P的坐标为（3，
），
∴|PA|•|PB|=4．
| 5 |
| π |
| 4 |
|
圆C的方程为p=2
| 5 |
| 5 |
（2）
|
| 5 |
| 2 |
∵点P的坐标为（3，
| 5 |
∴|PA|•|PB|=4．
点评：本小题主要考查参数方程、极坐标方程等基础知识，考查参数的几何意义，考查运算求解能力，属于中档题．
练习册系列答案
相关题目
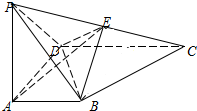如图，在四棱锥P-ABCD中，AD=CD=2AB=2，PA⊥AD，AB∥CD，CD⊥AD，E为PC的中点，且DE=EC．