题目内容
1．在公比为q且各项均为正数的等比数列{an}中，Sn为{an}的前n项和．若a1=$\frac{1}{{q}^{2}}$，且S5=S2+2，则q的值为$\frac{\sqrt{5}-1}{2}$．分析 由a1=$\frac{1}{{q}^{2}}$，且S5=S2+2，q＞0．可得a3+a4+a5=${a}_{1}{q}^{2}$（1+q+q2）=2，代入化简解出即可得出．
解答 解：∵a1=$\frac{1}{{q}^{2}}$，且S5=S2+2，q＞0．
∴a3+a4+a5=${a}_{1}{q}^{2}$（1+q+q2）=2，
∴q2+q-1=0，
解得q=$\frac{-1+\sqrt{5}}{2}$．
故答案为：$\frac{\sqrt{5}-1}{2}$．
点评 本题考查了等比数列的通项公式与求和公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
12．某公司在销售某种环保材料过程中，记录了每日的销售量x（吨）与利润y（万元）的对应数据，下表是其中的几组对应数据，由此表中的数据得到了y关于x的线性回归方程$\widehat{y}$=0.7x+a，若每日销售量达到10吨，则每日利润大约是（ ）
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
| A． | 7.2万元 | B． | 7.35万元 | C． | 7.45万元 | D． | 7.5万元 |
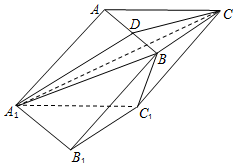如图，在底边为等边三角形的斜三棱柱ABC-A1B1C1中，AA1=$\sqrt{3}$AB，四边形B1C1CB为矩形，过A1C做与直线BC1平行的平面A1CD交AB于点D．