题目内容
5．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足$\overrightarrow{a}$•$\overrightarrow{b}$=1，|$\overrightarrow{a}$|=2，|$\overrightarrow{b}$|=3，则|$\overrightarrow{a}$-$\overrightarrow{b}$|=（ ）| A． | $\sqrt{13}$ | B． | 6 | C． | $\sqrt{11}$ | D． | 5 |
分析 根据平面向量数量积的定义与模长公式，求模长|$\overrightarrow{a}$-$\overrightarrow{b}$|即可．
解答 解：向量$\overrightarrow{a}$，$\overrightarrow{b}$满足$\overrightarrow{a}$•$\overrightarrow{b}$=1，|$\overrightarrow{a}$|=2，|$\overrightarrow{b}$|=3，
∴${（\overrightarrow{a}-\overrightarrow{b}）}^{2}$=${\overrightarrow{a}}^{2}$-2$\overrightarrow{a}$$•\overrightarrow{b}$+${\overrightarrow{b}}^{2}$=22-2×1+32=11，
∴|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{11}$．
故选：C．
点评 本题考查了平面向量数量积与模长公式的应用问题，是基础题．
练习册系列答案
导学教程高中新课标系列答案
相关题目
13．复数$z=|{（{\sqrt{3}-i}）i}|+{i^{2017}}$（i为虚数单位），则复数z的共轭复数为（ ）
| A． | 2-i | B． | 2+i | C． | 4-i | D． | 4+i |
20．若 数列$\left\{{a_n}\right\}满足{a_1}=2，{a_{n+1}}=\frac{{1+{a_n}}}{{1-{a_n}}}（n∈{N^*}）$，则该数列的前2017项的乘积是（ ）
| A． | -2 | B． | -3 | C． | 2 | D． | $-\frac{1}{2}$ |
10．椭圆$C：\frac{x^2}{4}+\frac{y^2}{3}=1$与双曲线$E：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a，b＞0）$有相同的焦点，且两曲线的离心率互为倒数，则双曲线渐近线的倾斜角的正弦值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $\frac{{\sqrt{3}}}{3}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
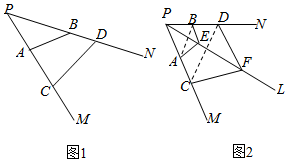平面上，点A、C为射线PM上的两点，点B、D为射线PN上的两点，则有$\frac{{{S_{△PAB}}}}{{{S_{△PCD}}}}=\frac{PA•PB}{PC•PD}$（其中S△PAB、S△PCD分别为△PAB、△PCD的面积）；空间中，点A、C为射线PM上的两点，点B、D为射线PN上的两点，点E、F为射线PL上的两点，则有$\frac{{{V_{P-ABE}}}}{{{V_{P-CDF}}}}$=$\frac{PA•PB•PE}{PC•PD•PF}$（其中VP-ABE、VP-CDF分别为四面体P-ABE、P-CDF的体积）．
14．若复数z满足$（z-1）i=\sqrt{2}$（i为虚数单位），则复数|z|=（ ）
| A． | 1 | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | $2\sqrt{2}$ |
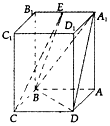在四棱柱ABCD-A1B1C1D1中，四边形ABCD为平行四边形，AA1⊥平面ABCD，∠BAD=60°，AB=2，BC=1．AA1=$\sqrt{6}$，E为A1B1的中点．