题目内容
20.若 数列$\left\{{a_n}\right\}满足{a_1}=2,{a_{n+1}}=\frac{{1+{a_n}}}{{1-{a_n}}}(n∈{N^*})$,则该数列的前2017项的乘积是( )| A. | -2 | B. | -3 | C. | 2 | D. | $-\frac{1}{2}$ |
分析 数列$\left\{{a_n}\right\}满足{a_1}=2,{a_{n+1}}=\frac{{1+{a_n}}}{{1-{a_n}}}(n∈{N^*})$,可得:an+4=an,a1a2a3a4=1.利用周期性即可得出.
解答 解:∵数列$\left\{{a_n}\right\}满足{a_1}=2,{a_{n+1}}=\frac{{1+{a_n}}}{{1-{a_n}}}(n∈{N^*})$,
∴a2=$\frac{1+{a}_{1}}{1-{a}_{1}}$=-3,同理可得:a3=$-\frac{1}{2}$,a4=$\frac{1}{3}$,a5=2,….
∴an+4=an,a1a2a3a4=1.
∴该数列的前2017项的乘积=1504×a1=2.
故选:C.
点评 本题考查了数列递推关系、数列的周期性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
16.在(1+x)+(1+x)2+(1+x)3+…+(1+x)11的展开式中,x2的系数是( )
| A. | 55 | B. | 66 | C. | 165 | D. | 220 |
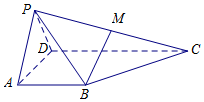 在四棱锥DN⊥平面PBC中,平面PAD⊥平面ABCD,△PAD为等边三角形,AB=AD=$\frac{1}{2}$CD=2,AB⊥AD,AB∥CD,点M是PC的中点.
在四棱锥DN⊥平面PBC中,平面PAD⊥平面ABCD,△PAD为等边三角形,AB=AD=$\frac{1}{2}$CD=2,AB⊥AD,AB∥CD,点M是PC的中点.