题目内容
14.若复数z满足$(z-1)i=\sqrt{2}$(i为虚数单位),则复数|z|=( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $2\sqrt{2}$ |
分析 利用代数的运算性质求出复数z,再求z的模长|z|.
解答 解:复数z满足$(z-1)i=\sqrt{2}$(i为虚数单位),
∴z-1=$\frac{\sqrt{2}}{i}$=-$\sqrt{2}$i
∴z=1-$\sqrt{2}$i
∴复数|z|=$\sqrt{{1}^{2}{+(-\sqrt{2})}^{2}}$=$\sqrt{3}$.
故选:C.
点评 本题考查了复数的代数运算与模长的计算问题,是基础题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
5.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{a}$•$\overrightarrow{b}$=1,|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=3,则|$\overrightarrow{a}$-$\overrightarrow{b}$|=( )
| A. | $\sqrt{13}$ | B. | 6 | C. | $\sqrt{11}$ | D. | 5 |
19.设函数f(x)=ex(x3-a)(a∈R)在(-3,0)单调递减,则a的范围是( )
| A. | [0,+∞) | B. | [2,4] | C. | [4,+∞) | D. | (2,4) |
3.若a∈[1,6],则函数$y=\frac{{{x^2}+a}}{x}$在区间[2,+∞)内单调递增的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
4.函数y=2cos2x-sin2x的最小值是( )
| A. | -2 | B. | $1-\sqrt{2}$ | C. | $1+\sqrt{2}$ | D. | 2 |
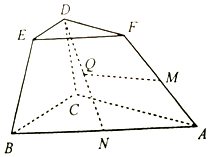 如图,在棱台ABC-FED中,△DEF与△ABC分别是棱长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,N为AB中点,$\overrightarrow{AM}=λ\overrightarrow{AF}({λ∈R,λ>0})$.
如图,在棱台ABC-FED中,△DEF与△ABC分别是棱长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,N为AB中点,$\overrightarrow{AM}=λ\overrightarrow{AF}({λ∈R,λ>0})$.