题目内容
2. (Ⅰ)求过点($\sqrt{3},2\sqrt{2}$)且与双曲线$\frac{x^2}{9}-\frac{y^2}{16}=1$有相同渐近线的双曲线的标准方程.
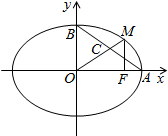
(Ⅰ)求过点($\sqrt{3},2\sqrt{2}$)且与双曲线$\frac{x^2}{9}-\frac{y^2}{16}=1$有相同渐近线的双曲线的标准方程.(Ⅱ) 如图所示,A、B是椭圆的两个顶点,C是AB的中点,F为椭圆的右焦点,OC的延长线交椭圆于点M,且|OF|=$\sqrt{2}$,若MF⊥OA,求此椭圆的标准方程.
分析 (Ⅰ)设$\frac{x^2}{9}-\frac{y^2}{16}=λ(λ≠0)$,代入点($\sqrt{3},2\sqrt{2}$),解得$λ=-\frac{1}{6}$,可得双曲线的标准方程.
(Ⅱ)设所求椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),求出M点的坐标为($\sqrt{2}$,$\frac{b^2}{a}$),利用O、C、M三点共线,求出a,b,即可求此椭圆的标准方程.
解答 解:(Ⅰ)设$\frac{x^2}{9}-\frac{y^2}{16}=λ(λ≠0)$,代入点($\sqrt{3},2\sqrt{2}$),解得$λ=-\frac{1}{6}$
∴$\frac{{3{y^2}}}{8}-\frac{{2{x^2}}}{3}=1$ ….(6分)
(Ⅱ)设所求椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),则A(a,0),B(0,b),C($\frac{a}{2}$,$\frac{b}{2}$),F(c,0)
依题意得c=$\sqrt{2}$,即a2-b2=2.
又MF⊥OA,则FM所在的直线方程是x=$\sqrt{2}$,代入椭圆方程得y=±$\frac{b^2}{a}$,所以M点的坐标为($\sqrt{2}$,$\frac{b^2}{a}$)
由于O、C、M三点共线,所以$\frac{{\frac{b^2}{a}}}{{\sqrt{2}}}$=$\frac{\frac{b}{2}}{\frac{a}{2}}$,即$b=\sqrt{2}$,所以a2=4,b2=2.
所以所求椭圆的标准方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$. ….(12分)
点评 本题考查双曲线、椭圆的标准方程,考查待定系数法的运用,考查学生分析解决问题的能力,属于中档题.

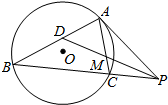 如图所示,△ABC内接于圆O,过点A的切线交BC的延长线于点P,D为AB的中点,DP交AC于点M,若BP=8,AM=4,AC=6,则PA=( )
如图所示,△ABC内接于圆O,过点A的切线交BC的延长线于点P,D为AB的中点,DP交AC于点M,若BP=8,AM=4,AC=6,则PA=( )| A. | 4$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | 5$\sqrt{2}$ |
| A. | $\frac{{\sqrt{21}}}{3}$ | B. | 2 | C. | $\frac{{\sqrt{6}}}{2}$ | D. | $\frac{5}{3}$ |
 如图所示,已知矩形ABCD与ABEF全等,D-AB-E为直二面角,M为AB的中点,FM与BD所成角为θ,且cosθ=$\frac{\sqrt{3}}{9}$,则AB与BC的长度之比为( )
如图所示,已知矩形ABCD与ABEF全等,D-AB-E为直二面角,M为AB的中点,FM与BD所成角为θ,且cosθ=$\frac{\sqrt{3}}{9}$,则AB与BC的长度之比为( )| A. | 1:1 | B. | $\sqrt{2}$:1 | C. | $\sqrt{2}$:2 | D. | 1:2 |
 在棱长为1的正方体ABCD-A1B1C1D1中,点P是它的体对角线BD1上一动点,则|AP|+|PC|的最小值是$\frac{2\sqrt{6}}{3}$.
在棱长为1的正方体ABCD-A1B1C1D1中,点P是它的体对角线BD1上一动点,则|AP|+|PC|的最小值是$\frac{2\sqrt{6}}{3}$.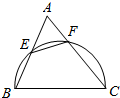 如图,△ABC中,BC=10,以 BC 为直径的圆分别交 AB,AC于点 E,F.
如图,△ABC中,BC=10,以 BC 为直径的圆分别交 AB,AC于点 E,F.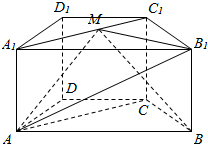 在四棱柱ABCD-A1B1C1D1中,底面ABCD为梯形,AB∥CD,AD=DC=CB=1,∠ABC=$\frac{π}{3}$,对角面A1ACC1为矩形,平面A1ACC1⊥平面ABCD,CC1=1.
在四棱柱ABCD-A1B1C1D1中,底面ABCD为梯形,AB∥CD,AD=DC=CB=1,∠ABC=$\frac{π}{3}$,对角面A1ACC1为矩形,平面A1ACC1⊥平面ABCD,CC1=1.