题目内容
7.南山中学近几年规模不断壮大,学生住宿异常紧张,学校拟用1000万元购一块空地,计划在该空地上建造一栋至少8层,每层2000平方米的学生电梯公寓.经测算,如果将公寓建为x(x≥8)层,则每平方米的平均建筑费用为560+48x(单位:元).(1)写出拟修公寓每平米的平均综合费用y关于建造层数x的函数关系式;
(2)该公寓应建造多少层时,可使公寓每平方米的平均综合费用最少?最少值是多少?(结果精确到1元)
(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用=$\frac{购地总费用}{建筑总面积}$)
分析 (1)由已知得,楼房每平方米的平均综合费为每平方米的平均建筑费用为560+48x与平均购地费用的和,由已知中某单位用107元购得一块空地,计划在该地块上建造一栋x层,每层2000平方米的楼房,我们易得楼房平均综合费用y关于建造层数x的函数关系式;
(2)由(1)中的楼房平均综合费用y关于建造层数x的函数关系式,要求楼房每平方米的平均综合费用最小值,先利用基本不等式,检验等号成立的条件,即可求最小值.
解答 解(1)依题意得y=(560+48x)+$\frac{1000×10000}{2000x}$
=560+48x+$\frac{5000}{x}$(x≥8,x∈N*);
(2)由y=560+48x+$\frac{5000}{x}$≥560+2$\sqrt{48x•\frac{5000}{x}}$=560+400$\sqrt{6}$,
当且仅当48x=$\frac{5000}{x}$,即x=$\frac{25}{\sqrt{6}}$∈(10,11),取得等号,
由于x≥8,x∈N*,
故由x=10时,y=1540;x=11时,y=1543.
故该公寓应建造10层时,可使公寓每平方米的平均综合费用最少,最小值为1540元.
点评 函数的实际应用题,我们要经过审题→建模→解模→还原四个过程,在建模时要注意实际情况对自变量x取值范围的限制,解模时也要实际问题实际考虑.将实际的最大(小)化问题,利用函数模型,转化为求函数的最大(小)是最优化问题中,最常见的思路之一.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
12.函数$f(x)=\sqrt{1-{{log}_2}(x-1)}$的定义域为( )
| A. | (1,3] | B. | (-∞,3] | C. | (0,3] | D. | (1,3) |
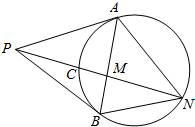
 如图所示,已知PBD是⊙O的割线,PA、PC是⊙O的切线,A、C为切点,求证:
如图所示,已知PBD是⊙O的割线,PA、PC是⊙O的切线,A、C为切点,求证: 设A(x0,y0)(x0,y0≠0)是椭圆T:$\frac{{x}^{2}}{m+1}$+y2=1(m>0)上一点,它关于y轴、原点、x轴的对称点依次为B,C,D.E是椭圆T上不同于A的另外一点,且AE⊥AC,如图所示.
设A(x0,y0)(x0,y0≠0)是椭圆T:$\frac{{x}^{2}}{m+1}$+y2=1(m>0)上一点,它关于y轴、原点、x轴的对称点依次为B,C,D.E是椭圆T上不同于A的另外一点,且AE⊥AC,如图所示. 如图,正方形ABCD被两条与边平行的线段EF、GH分割成4个小矩形,P是EF与GH的交点,若矩形PFCH的面积恰好是矩形AGPE面积的2倍,试确定∠HAF的大小,并证明你的结论.
如图,正方形ABCD被两条与边平行的线段EF、GH分割成4个小矩形,P是EF与GH的交点,若矩形PFCH的面积恰好是矩形AGPE面积的2倍,试确定∠HAF的大小,并证明你的结论.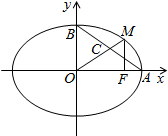 (Ⅰ)求过点($\sqrt{3},2\sqrt{2}$)且与双曲线$\frac{x^2}{9}-\frac{y^2}{16}=1$有相同渐近线的双曲线的标准方程.
(Ⅰ)求过点($\sqrt{3},2\sqrt{2}$)且与双曲线$\frac{x^2}{9}-\frac{y^2}{16}=1$有相同渐近线的双曲线的标准方程.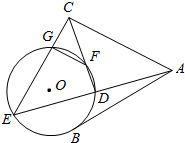 如图,AB是⊙O的一条切线,切点为B,ADE,CFD和 CGE都是⊙O的割线,AC=AB
如图,AB是⊙O的一条切线,切点为B,ADE,CFD和 CGE都是⊙O的割线,AC=AB