题目内容
11.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左,右焦点为F1,F2.A,B为顶点,以线段F1F2为直径的圆交双曲线的一条渐近线bx-ay=0于M,N两点,且∠MAB=30°,则双曲线的离心率为( )| A. | $\frac{{\sqrt{21}}}{3}$ | B. | 2 | C. | $\frac{{\sqrt{6}}}{2}$ | D. | $\frac{5}{3}$ |
分析 由题意求出圆的方程,双曲线的渐近线方程,通过∠MAB=30°求出a,b的关系,然后求出双曲线的离心率.
解答  解:由题意可知,圆的方程为x2+y2=c2,双曲线的渐近线方程为y=$\frac{b}{a}$x,
解:由题意可知,圆的方程为x2+y2=c2,双曲线的渐近线方程为y=$\frac{b}{a}$x,
将其代入圆的方程得M(a,b),N(-a,-b).因为∠BAM=30°.
连接MB,在Rt△MAB中,tan∠BAM=$\frac{b}{2a}$=$\frac{\sqrt{3}}{3}$,
所以$\frac{b}{a}$=$\frac{2\sqrt{3}}{3}$,
所以e=$\frac{c}{a}$=$\sqrt{1+\frac{4}{3}}$=$\frac{\sqrt{21}}{3}$.
故选:A.
点评 本题考查双曲线的简单性质,考查圆的方程的应用,考查计算能力.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
6.已知两定点A(-2,1),B(1,3),动点P在直线x-y+1=0上,当|PA|+|PB|取最小值时,这个最小值为( )
| A. | $\sqrt{5}$ | B. | 3 | C. | $\sqrt{13}$ | D. | $\sqrt{17}$ |
 如图,⊙O的半径OC垂直于直径AB,M为OB上一点,CM的延长线交⊙O于N,过N点的切线交AB的延长线于P.
如图,⊙O的半径OC垂直于直径AB,M为OB上一点,CM的延长线交⊙O于N,过N点的切线交AB的延长线于P.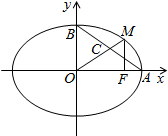 (Ⅰ)求过点($\sqrt{3},2\sqrt{2}$)且与双曲线$\frac{x^2}{9}-\frac{y^2}{16}=1$有相同渐近线的双曲线的标准方程.
(Ⅰ)求过点($\sqrt{3},2\sqrt{2}$)且与双曲线$\frac{x^2}{9}-\frac{y^2}{16}=1$有相同渐近线的双曲线的标准方程.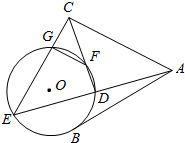 如图,AB是⊙O的一条切线,切点为B,ADE,CFD和 CGE都是⊙O的割线,AC=AB
如图,AB是⊙O的一条切线,切点为B,ADE,CFD和 CGE都是⊙O的割线,AC=AB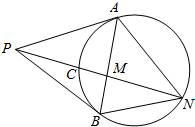
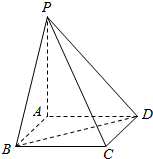 已知PA垂直于矩形ABCD所在平面,PA=3,AB=1,BC=$\sqrt{3}$.
已知PA垂直于矩形ABCD所在平面,PA=3,AB=1,BC=$\sqrt{3}$.