题目内容
函数f(x)=2x,对于20个数:a1,a2,…,a10;b1,b2,…,b10∈[0,1],且满足:
f2(ai)=
f2(bi),则
的最小值是( )
| 10 |
 |
| i=1 |
| 10 |
 |
| i=1 |
| |||
|
A、
| ||
B、
| ||
C、
| ||
| D、1 |
考点:二维形式的柯西不等式
专题:计算题,不等式的解法及应用
分析:先考虑两个数的情况:m1=2a1,m2=2a2,n1=2b1,n2=2b2,由题意得,m12+m22=n12+n22=r2.m1,m2,n1,n2∈[1,2],设
=(m1,m2),
=(n1,n2),运用向量的夹角公式,当取
=(1,2),
=(2,1),
=
≤cos<
,
>≤1.然后再推广,即可得到最小值.
| x1 |
| x2 |
| x1 |
| x2 |
| (1,2)•(2,1) |
| 12+22 |
| 4 |
| 5 |
| x1 |
| x2 |
解答:
解:先考虑两个数的情况:
m1=2a1,m2=2a2,n1=2b1,n2=2b2,
由题意得,m12+m22=n12+n22=r2.
m1,m2,n1,n2∈[1,2],
设
=(m1,m2),
=(n1,n2),
则
=
,
=
=cos<
,
>,
当取
=(1,2),
=(2,1),
=
≤cos<
,
>≤1.
推广:当
=(1,1,2,2),
=(2,2,1,1),
即有
=
≤cos<
,
>≤1.
…
当
=(1,1,1,1,1,2,2,2,2,2),
=(2,2,2,2,2,1,1,1,1,1),
即有
=
≤cos<
,
>≤1.
则所求的最小值为
.
故选B.
m1=2a1,m2=2a2,n1=2b1,n2=2b2,
由题意得,m12+m22=n12+n22=r2.
m1,m2,n1,n2∈[1,2],
设
| x1 |
| x2 |
则
| f(a1)f(b1)+f(a2)f(b2) |
| f2(a1)+f2(a2) |
| m1n1+m2n2 |
| m12+m22 |
=
| ||||
|
|
| x1 |
| x2 |
当取
| x1 |
| x2 |
| (1,2)•(2,1) |
| 12+22 |
| 4 |
| 5 |
| x1 |
| x2 |
推广:当
| x1 |
| x2 |
即有
| 2+2+2+2 |
| 12+12+22+22 |
| 4 |
| 5 |
| x1 |
| x2 |
…
当
| x1 |
| x2 |
即有
| 2+2+…+2 |
| 12+12+…+22 |
| 4 |
| 5 |
| x1 |
| x2 |
则所求的最小值为
| 4 |
| 5 |
故选B.
点评:本题考查柯西不等式及运用,考查运用向量的方法,求最值,注意先从最简单的情况考虑,考查运算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
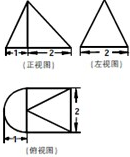
一个几何体的三视图如图,其俯视图是一个等边三角形,则这个几何体的体积为( )

A、
| ||||
B、
| ||||
C、
| ||||
D、(4+π)
|
抛物线y=2x2上一点P到焦点的距离为1,则点P的坐标为( )
A、(
| ||||||
B、(
| ||||||
C、(-
| ||||||
D、(±
|
 如图所示,四棱锥P-ABCD的底面ABCD为直角梯形,且AD∥BC,AD⊥AB,E是PC的中点,PA=BC=2AD=1,AB=2,∠PAB=120°,∠PBC=90°.
如图所示,四棱锥P-ABCD的底面ABCD为直角梯形,且AD∥BC,AD⊥AB,E是PC的中点,PA=BC=2AD=1,AB=2,∠PAB=120°,∠PBC=90°.