题目内容

5．某几何体的三视图如图所示，则该几何体的表面积为（　　）
A．44B．32C．10+6$\sqrt{17}$D．22+6$\sqrt{17}$

分析 根据几何体的三视图，得出该几何体是底面为矩形四棱锥，结合图中数据求出它的表面积．

解答 解：根据几何体的三视图知，该几何体是底面为矩形四棱锥；
且矩形的长为6，宽为2，四棱锥的高为4，如图所示：

所以该四棱锥的表面积为
S=S矩形ABCD+2S△PAB+2S△PBC
=6×2+2×$\frac{1}{2}$×6×$\sqrt{{4}^{2}{+1}^{2}}$+2×$\frac{1}{2}$×2×$\sqrt{{4}^{2}{+3}^{2}}$
=22+6$\sqrt{17}$．
故选：D．

点评 本题考查了利用空间几何体的三视图求表面积的应用问题，是基础题目．

练习册系列答案
相关题目
1．函数上y=lnx的点到直线x-y+1=0的距离的最小值是$\sqrt{2}$．
16．设甲、乙两个圆锥的底面积分别为S1，S2，母线长分别为L1，L2，若它们的侧面积相等，且$\frac{{S}_{1}}{{S}_{2}}$=$\frac{9}{4}$，则$\frac{L_1}{L_2}$的值是$\frac{2}{3}$．
13．某三棱锥的三视图如图所示，则该三棱锥的体积是（　　）
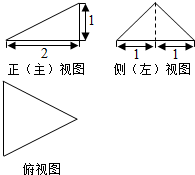
A．$\frac{2}{3}$B．2C．$\sqrt{3}$D．$\frac{{\sqrt{3}}}{3}$
20．某校选定甲、乙、丙、丁、戊共5名教师去3个边远地区支教（每地至少1人），其中甲和乙一定不同地，甲和丙必须同地，则不同的选派方案共有（　　）种．
A．27B．30C．33D．36
10．六个人从左到右排成一列，其中甲、乙两人至少有一人在两端的排法总数有（　　）
A．48种B．384种C．432种D．288种
17．已知函数$f（x）=\frac{{{x^2}-6x+4a}}{4x}-lnx$，其中a∈R
（1）若函数f（x）在（0，+∞）单调递增，求实数a的取值范围
（2）若曲线y=f（x）在点（1，f（1））处的切线垂直于y轴，求函数f（x）的单调区间与极值．
14．对于函数y=f（x），若存在定义域D内某个区间[a，b]，使得y=f（x）在[a，b]上的值域也是[a，b]，则称函数y=f（x）在定义域D上封闭．如果函数$f（x）=\frac{kx}{1+|x|}$（k≠0）在R上封闭，那么实数k的取值范围是（1，+∞）．
15．如图，正方形ABCD边长为2，以D为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F，连结CF并延长交AB于点E．
（Ⅰ）求证：|AE|=|EB|；
（Ⅱ）求|EF|•|FC|的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网