题目内容
2.设数列{an}的前n项和为Sn,且a1=1,an+1=2Sn+3,则S4=66.分析 利用递推关系与等比数列的通项公式及其前n项和公式即可得出.
解答 解:∵an+1=2Sn+3,
∴an=2Sn-1+3(n≥2),
可得an+1-an=2an,即an+1=3an,n≥2,
∴数列{an}从第二项起是公比为3的等比数列,a2=5,
∴${S_4}=1+\frac{{5(1-{3^3})}}{1-3}$=66.
故答案为:66.
点评 本题考查了等比数列的通项公式及其前n项和公式、递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
13.某三棱锥的三视图如图所示,则该三棱锥的体积是( )
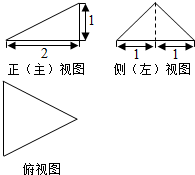

| A. | $\frac{2}{3}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
10.六个人从左到右排成一列,其中甲、乙两人至少有一人在两端的排法总数有( )
| A. | 48种 | B. | 384种 | C. | 432种 | D. | 288种 |