题目内容
设正项等比数列{an}的首项a1=
,a10=
,前n项和为Sn.
(1)求{an}的通项及Sn
(2)求{nSn}的前n项和Tn.
| 1 |
| 2 |
| 1 |
| 1024 |
(1)求{an}的通项及Sn
(2)求{nSn}的前n项和Tn.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)利用等比数列的通项公式即可得到q;然后求解通项公式及Sn
(2)利用等比数列的前n项和公式即可得到Sn,再利用“错位相减法”即可得到数列{nSn}的前n项和Tn.
(2)利用等比数列的前n项和公式即可得到Sn,再利用“错位相减法”即可得到数列{nSn}的前n项和Tn.
解答:
解:因为正项等比数列{an}的首项a1=
,a10=
,
所以q=
.∴an=a1qn-1=
,
Sn=
=1-
.
(2)由题意可知nSn=n-
,
{nSn}的前n项和Tn.
∴Tn=(1+2+3+…+n)-(
+
+
+…+
)…①,
Tn=
(1+2+3+…+n)-(
+
+…+
+
)…②
①-②得:
Tn=
-(
+
+
+…+
-
)
=
-
+
=
-1+
,
∴Tn=
+
-2
| 1 |
| 2 |
| 1 |
| 1024 |
所以q=
| 1 |
| 2 |
| 1 |
| 2n |
Sn=
| ||||
1-
|
| 1 |
| 2n |
(2)由题意可知nSn=n-
| n |
| 2n |
{nSn}的前n项和Tn.
∴Tn=(1+2+3+…+n)-(
| 1 |
| 2 |
| 2 |
| 22 |
| 3 |
| 23 |
| n |
| 2n |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 2 |
| 23 |
| n-1 |
| 2n |
| n |
| 2n+1 |
①-②得:
| 1 |
| 2 |
| n(n+1) |
| 4 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
| n |
| 2n+1 |
=
| n(n+1) |
| 4 |
| ||||
1-
|
| n |
| 2n+1 |
| n(n+1) |
| 4 |
| n+2 |
| 2n+1 |
∴Tn=
| n(n+1) |
| 2 |
| n+2 |
| 2n |
点评:本题考查数列的求和,熟练掌握等比数列的通项公式、等比数列的前n项和公式、“错位相减法”是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
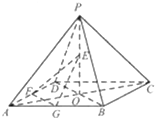 如图,四棱锤P-ABCD的底面为正方形,每题侧棱的长都等于底面的长,AC∩BD=O,E、F、G分别是PO、AD、AB的中点.
如图,四棱锤P-ABCD的底面为正方形,每题侧棱的长都等于底面的长,AC∩BD=O,E、F、G分别是PO、AD、AB的中点.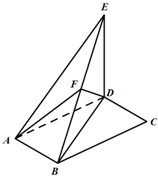 如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4,将△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD.
如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4,将△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD.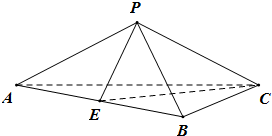 如图,在三棱锥P-ABC中,AB=2
如图,在三棱锥P-ABC中,AB=2