题目内容
已知f（x）=ax-2，g（x）=loga|x|，（a＞0且a≠1），若f（4）•g（-4）＜0，则y=f（x），y=g（x）在同一坐标系内的大致图象是（ ）
A、 |
B、 |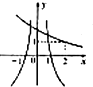
C、 |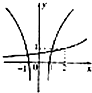
D、 |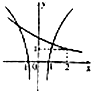
考点：函数的图象
专题：函数的性质及应用
分析：观察两个函数的解析式，f（x）=ax-2是指数型的，g（x）=loga|x|是对数型的且是一个偶函数，由f（4）•g（-4）＜0，可得出g（-4）＜0，由这些特征对选项进行正确判断即可
解答：
解：由题意f（x）=ax-2是指数型的，g（x）=loga|x|是对数型的且是一个偶函数，
由f（4）•g（-4）＜0，可得出g（-4）＜0，由此特征可以确定C、D两选项不正确，
A，B两选项中，在（0，+∞）上，函数是减函数，
故其底数a∈（0，1）由此知f（x）=ax-2，是一个减函数，由此知A不对，B选项是正确答案
故选B
由f（4）•g（-4）＜0，可得出g（-4）＜0，由此特征可以确定C、D两选项不正确，
A，B两选项中，在（0，+∞）上，函数是减函数，
故其底数a∈（0，1）由此知f（x）=ax-2，是一个减函数，由此知A不对，B选项是正确答案
故选B
点评：本题考查识图，判断图的能力，考查根据函数的图象确定函数的性质及通过函数的解析式推测函数的图象，综合性较强，解决此类题关键是找准最明显的特征作为切入点如本题选择了从f（4）•g（-4）＜0，因为f（4）一定为正，这可以由函数是指数型的函数轻易得出．
练习册系列答案
名校课堂系列答案
相关题目
用三段论推理：“指数函数y=ax是增函数，因为y=（
）x是指数函数，所以y=（
）x是增函数”，你认为这个推理（ ）
| 1 |
| 2 |
| 1 |
| 2 |
| A、大前提错误 |
| B、小前提错误 |
| C、推理形式错误 |
| D、是正确的 |
定义在R上的奇函数y=f（x）满足不等式：
＞0(x1≠x2)，若当a＞0时，f（a2）+f（b2-1）＜0，则
的取值范围是（ ）
| f(x2)-f(x1) |
| x2-x1 |
| (a+1)2+b2 |
| A、（0，2） | ||
| B、（1，2） | ||
C、（0，
| ||
D、（1，
|