题目内容
若集合P={x|x=3k-2,k∈Z},Q={x|x=6n+1,n∈Z},试判断P、Q的包含关系并证明.
考点:集合的包含关系判断及应用
专题:集合
分析:由已知中集合P={x|x=3k-2,k∈Z},Q={x|x=6n+1,n∈Z},易判断出若x∈Q,则x∈P,即Q⊆P,再举出反例4,可得P?Q,进而得到结论.
解答:
解:Q?P,理由如下:
若x∈Q,则x=6n+1=3•(2n)+1=3•(2n+1)-2,
∵n∈Z,
∴2n+1∈Z,
即x∈P
故Q⊆P
存在4∈P,但4∉Q
故P?Q
故Q?P
若x∈Q,则x=6n+1=3•(2n)+1=3•(2n+1)-2,
∵n∈Z,
∴2n+1∈Z,
即x∈P
故Q⊆P
存在4∈P,但4∉Q
故P?Q
故Q?P
点评:本题考查的知识点是集合的包含关系判断,熟练掌握集合包含关系及真包含关系的定义是解答的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
变量x,y满足约束条件
,则x+3y最大值是( )
|
| A、2 | B、3 | C、4 | D、5 |
航空母舰“辽宁舰”在某次舰载机起降飞行训练中,有5架歼-15飞机准备着舰.如果甲、乙两机必须相邻着舰,而甲、丁两机不能相邻着舰,那么不同的着舰方法有( )
| A、12种 | B、16种 |
| C、24种 | D、36种 |
 设△ABC是边长为1的正三角形,点P1,P2,P3四等分线段BC(如图所示).
设△ABC是边长为1的正三角形,点P1,P2,P3四等分线段BC(如图所示).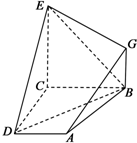 如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=
如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=