题目内容
5. 如题(19)图,四边形ABCD为菱形,四边形BDEF为F平行四边形,平面BDEF⊥平面ACE,设AC∩BD=O,AB=AC=2,BF=$\sqrt{3}$.
如题(19)图,四边形ABCD为菱形,四边形BDEF为F平行四边形,平面BDEF⊥平面ACE,设AC∩BD=O,AB=AC=2,BF=$\sqrt{3}$.(Ⅰ)证明:平面BDEF⊥平面ABCD,
(Ⅱ)若点D到平面ACE的距离为$\frac{\sqrt{3}}{2}$,求二面角C-EF-O的正切值.
分析 (Ⅰ)根据面面垂直的判定定理证明AC⊥平面BDEF即可证明平面BDEF⊥平面ABCD,
(Ⅱ)根据二面角平面角的定义,作出二面角的平面角,结合三角形的边角关系进行求解即可.
解答 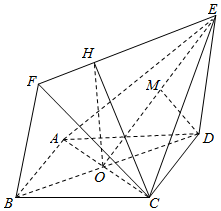 (Ⅰ)证明:∵四边形ABCD为菱形,
(Ⅰ)证明:∵四边形ABCD为菱形,
∴AC⊥BD,
∵平面BDEF⊥平面ACE,
∴AC⊥平面BDEF,
∵AC?平面ABCD,
∴平面BDEF⊥平面ABCD;
(Ⅱ)∵平面BDEF⊥平面ACE,
∴过D作DM⊥OE,则DM⊥平面ACE,
则DM是点D到平面ACE的距离,即DM=$\frac{\sqrt{3}}{2}$,
∵AB=AC=2,BF=$\sqrt{3}$,
∴OD=$\sqrt{3}$,OM=$\sqrt{O{D}^{2}-O{M}^{2}}$=$\frac{3}{2}$,
则OE=2OM=3,
∵DM=$\frac{\sqrt{3}}{2}$,∴∠DOM=30°,即∠FEO=∠DOM=30°,
过O作OH⊥FH与H,连接CH,
则∠CHO是二面角C-EF-O平面角,
OH=$\frac{1}{2}$OE=$\frac{3}{2}$,
则tan∠CHO=$\frac{OC}{OH}$=$\frac{1}{\frac{3}{2}}$=$\frac{2}{3}$,
即二面角C-EF-O的正切值是$\frac{2}{3}$.
点评 本题主要考查面面垂直的判断以及二面角的求解,根据面面垂直的判定定理证明线面垂直以及作出二面角的平面角是解决本题的关键.考查学生的推理能力.

练习册系列答案
相关题目
15.已知F1、F2分别是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点,过点F1的直线与双曲线C的左、右两支分别交于P、Q两点,|F1P|、|F2P|、|F1Q|成等差数列,且∠F1PF2=120°,则双曲线C的离心率是( )
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{7}$ |
13.已知双曲线C1:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)经过抛物线C2:y2=2px(p>0)的焦点,且双曲线的渐近线与抛物线的准线围成一个等边三角形,则双曲线C1的离心率是( )
| A. | 2 | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
17.已知抛物线y2=2x的弦AB的中点坐标为(1,$\frac{\sqrt{2}}{2}$),则|AB|=( )
| A. | 3 | B. | $\sqrt{2}+1$ | C. | $\sqrt{3}+1$ | D. | 4 |
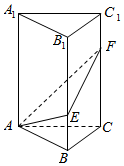 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,AA1=6,点E、F分别在棱BB1、CC1上,且BE=$\frac{1}{3}$BB1,C1F=$\frac{1}{3}$CC1.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,AA1=6,点E、F分别在棱BB1、CC1上,且BE=$\frac{1}{3}$BB1,C1F=$\frac{1}{3}$CC1.