题目内容
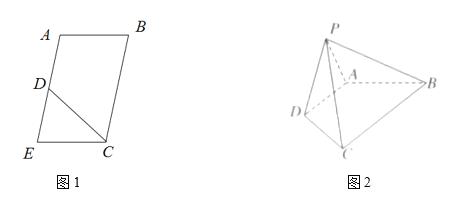
【题目】如图所示甲,在四边形ABCD中,![]() ,
,![]() ,
,![]() 是边长为8的正三角形,把
是边长为8的正三角形,把![]() 沿AC折起到
沿AC折起到![]() 的位置,使得平面
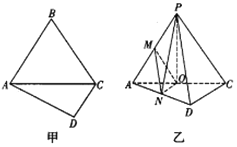
的位置,使得平面![]() 平面ACD,如图所示乙所示,点O,M,N分别为棱AC,PA,AD的中点.
平面ACD,如图所示乙所示,点O,M,N分别为棱AC,PA,AD的中点.
![]() 求证:
求证:![]() 平面PON;
平面PON;
![]() 求三棱锥
求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析;(2)4
【解析】
(1)根据平面与平面垂直,判断出![]() ,结合勾股定理及中位线,即可判断出
,结合勾股定理及中位线,即可判断出![]() ,进而判断出
,进而判断出![]() 平面PON。
平面PON。
(2)求得![]() ,结合点M到平面ANO的距离
,结合点M到平面ANO的距离![]() 、
、![]() 的值,
的值,![]() 即可。
即可。
![]() 如图所示,
如图所示,![]() 为正三角形,O为AC的中点,
为正三角形,O为AC的中点,
![]() ,
,
![]() 平面
平面![]() 平面ACD,平面
平面ACD,平面![]() 平面
平面![]() ,
,
![]() 平面ACD,
平面ACD,![]() 平面ACD,
平面ACD,
![]() .
.
![]() ,
,![]() ,
,![]() ,
,
![]() ,即
,即![]() .
.
![]() ,N分别为棱AC,AD的中点,
,N分别为棱AC,AD的中点,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() 平面PON;
平面PON;
![]() 解:由
解:由![]() ,
,![]() ,
,![]() ,可得
,可得![]() ,
,
![]() 点O、N分别是AC、AD的中点,
点O、N分别是AC、AD的中点,
![]() ,
,
![]() 是边长为8的等边三角形,
是边长为8的等边三角形,
![]() ,
,
又![]() 为PA的中点,
为PA的中点,
![]() 点M到平面ANO的距离
点M到平面ANO的距离![]() ,
,
![]() .
.
又![]() ,
,
![]() .
.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目