题目内容
【题目】已知函数:![]()
(I)当![]() 时,求
时,求![]() 的最小值;
的最小值;
(II)对于任意的![]() 都存在唯一的
都存在唯一的![]() 使得
使得![]() ,求实数a的取值范围.
,求实数a的取值范围.
【答案】(I)答案不唯一,见解析(II)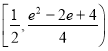
【解析】
(I)求导后,通过对![]() 的讨论,得到函数的单调性,根据单调性可得最小值;
的讨论,得到函数的单调性,根据单调性可得最小值;
(II)对于任意的![]() 都存在唯一的
都存在唯一的![]() 使得
使得![]() ,得
,得![]()
![]() 的值域是
的值域是![]() 的值域的子集,求出两个函数的值域后列式可求得.,注意
的值域的子集,求出两个函数的值域后列式可求得.,注意![]() 的唯一性满足
的唯一性满足
解:(I)![]()
![]() 时,
时,![]() 递增,
递增,![]() ,
,
![]() 时,
时,![]() 递减,
递减,![]()
![]() 时,
时,![]() 时
时![]() 递减,
递减,
![]() 时
时![]() 递增,
递增,
所以![]()
综上,当![]() ;
;
当![]()
当![]()
(II)因为对于任意的![]() 都存在唯一的
都存在唯一的![]() 使得
使得![]() 成立,
成立,
所以![]()
![]() 的值域是
的值域是![]() 的值域的子集.
的值域的子集.
因为![]()
![]() 递增,
递增,![]() 的值域为
的值域为![]()
(i)当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,
,
所以![]() 在[1,e]上的值域为
在[1,e]上的值域为![]() ,
,
所以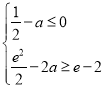
即![]()
(ii)当![]() 时,因为
时,因为![]() 时,
时,![]() 递减,
递减,![]() 时,
时,![]() 递增,且
递增,且![]() ,
,
所以只需![]()
即![]() ,所以
,所以![]()
(iii)当![]() 时,因为
时,因为![]() 在
在![]() 上单调递减,且
上单调递减,且![]() ,
,
所以不合题意.
综合以上,实数![]() 的取值范围是
的取值范围是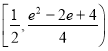 .
.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
【题目】某花店每天以每枝![]() 元的价格从农场购进若干枝玫瑰花,然后以每枝
元的价格从农场购进若干枝玫瑰花,然后以每枝![]() 元价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
元价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进![]() 枝玫瑰花,求当天的利润
枝玫瑰花,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:枝,
(单位:枝, ![]() )的函数解析式;
)的函数解析式;
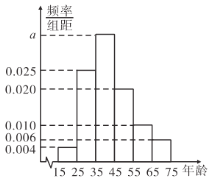
(2)花店记录了![]() 天玫瑰花的日需求量(单位:枝),整理得下表:
天玫瑰花的日需求量(单位:枝),整理得下表:
日需求量 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
以![]() 天的各需求量的频率作为各需求量发生的概率.
天的各需求量的频率作为各需求量发生的概率.
![]() 若花店一天购进
若花店一天购进![]() 枝玫瑰花,
枝玫瑰花, ![]() 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求![]() 的分布列, 数学期望及方差;
的分布列, 数学期望及方差;
![]() 若花店一天购进
若花店一天购进![]() 枝或
枝或![]() 枝玫瑰花,你认为应购进
枝玫瑰花,你认为应购进![]() 枝还是
枝还是![]() 枝?请说明理由.
枝?请说明理由.