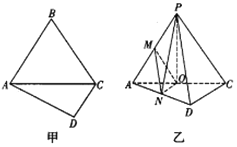
题目内容
【题目】在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是EA的中点(如图1),将
是EA的中点(如图1),将![]() 沿CD折起到图2中
沿CD折起到图2中![]() 的位置,得到四棱锥是
的位置,得到四棱锥是![]() .
.
(1)求证:![]() 平面PDA;
平面PDA;
(2)若PD与平面ABCD所成的角为![]() .且
.且![]() 为锐角三角形,求平面PAD和平面PBC所成锐二面角的余弦值.
为锐角三角形,求平面PAD和平面PBC所成锐二面角的余弦值.
【答案】(1)证明见解析; (2)![]()
【解析】
(1)证明![]() ,
,![]() ,即可证明线面垂直;
,即可证明线面垂直;
(2)由线面角求得![]() ,以
,以![]() 中点
中点![]() 为坐标原点建立直角坐标系,由向量法求得二面角的余弦值.
为坐标原点建立直角坐标系,由向量法求得二面角的余弦值.
(1)将![]() 沿CD折起过程中,
沿CD折起过程中,![]() 平面PDA成立.证明如下:
平面PDA成立.证明如下:
![]() 是EA的中点,
是EA的中点,![]() ,
,![]() ,
,
在![]() 中,由余弦定理得,
中,由余弦定理得,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 为等腰直角三角形且
为等腰直角三角形且![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() 平面PDA.
平面PDA.
(2)由(1)知![]() 平面PDA,
平面PDA,![]() 平面ABCD,
平面ABCD,
![]() 平面
平面![]() 平面ABCD,
平面ABCD,
![]() 为锐角三角形,
为锐角三角形,
![]() 在平面ABCD内的射影必在棱AD上,记为O,连接PO,
在平面ABCD内的射影必在棱AD上,记为O,连接PO,![]() 平面ABCD,
平面ABCD,
则![]() 是PD与平面ABCD所成的角,
是PD与平面ABCD所成的角,
![]() ,
,
![]() ,
,
![]() 为等边三角形,O为AD的中点,
为等边三角形,O为AD的中点,
故以O为坐标原点,过点O且与CD平行的直线为x轴,
DA所在直线为y轴,OP所在直线为z轴建立如图所示的空间直角坐标系,

设x轴与BC交于点M,
![]() ,
,![]()
易知![]()
![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() 平面PDA,
平面PDA,
![]() 可取平面PDA的一个法向量
可取平面PDA的一个法向量![]() ,
,
设平面PBC的法向量![]() ,
,
则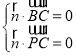 ,即
,即 ,
,
令![]() ,则
,则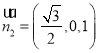 为平面PBC的一个法向量,
为平面PBC的一个法向量,
设平面PAD和平面PBC所成的角为![]() ,
,
由图易知![]() 为锐角,
为锐角,
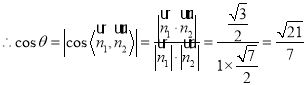 .
.
![]() 平面PAD和平面PBC所成角的余弦值为
平面PAD和平面PBC所成角的余弦值为![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】2018年11月21日,意大利奢侈品牌“![]() ﹠
﹠![]() ”在广告中涉嫌辱华,中国明星纷纷站出来抵制该品牌,随后京东、天猫、唯品会等中国电商平台全线下架了该品牌商品,当天有大量网友关注此事件,某网上论坛从关注此事件跟帖中,随机抽取了100名网友进行调查统计,先分别统计他们在跟帖中的留言条数,再把网友人数按留言条数分成6组:
”在广告中涉嫌辱华,中国明星纷纷站出来抵制该品牌,随后京东、天猫、唯品会等中国电商平台全线下架了该品牌商品,当天有大量网友关注此事件,某网上论坛从关注此事件跟帖中,随机抽取了100名网友进行调查统计,先分别统计他们在跟帖中的留言条数,再把网友人数按留言条数分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图;
,得到如图所示的频率分布直方图;

并将其中留言不低于40条的规定为“强烈关注”,否则为“一般关注”,对这100名网友进一步统计得到列联表的部分数据如下表.
一般关注 | 强烈关注 | 合计 | |
男 | 45 | ||
女 | 10 | 55 | |
合计 | 100 |
(1)在答题卡上补全列联表中数据;并判断能否有95%的把握认为网友对此事件是否为“强烈关注”与性别有关?
(2)现已从“强烈关注”的网友中按性别分层抽样选取了5人,再从这5人中选取2人,求这2人中至少有1名女性的概率.
参考公式及数据:![]() ,
,
| 0.05 | 0.010 |
| 3.841 | 6.635 |