题目内容
3.已知向量$\overrightarrow{a}$=(3,m),$\overrightarrow{b}$=(1,-2),若$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{b}$2,则m=-1.分析 利用两个向量的数量积公式,两个向量坐标形式的运算法则,求得m的值.
解答 解:∵向量$\overrightarrow{a}$=(3,m),$\overrightarrow{b}$=(1,-2),若$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{b}$2,则3-2m=5,
∴m=-1,
故答案为:-1.
点评 本题主要考查两个向量的数量积公式,两个向量坐标形式的运算法则,属于基础题.

练习册系列答案
相关题目
13.函数y=f(x)的图象向右平移$\frac{π}{3}$单位后与函数y=cos2x的图象重合,则y=f(x)的解析式是( )
| A. | f(x)=cos(2x$+\frac{π}{3}$) | B. | f(x)=-cos(2x-$\frac{π}{6}$) | C. | f(x)=-sin(2x+$\frac{π}{6}$) | D. | f(x)=sin(2x-$\frac{π}{6}$) |
18.若集合A={-2,0,1,3},B={-1,1,3}则A∪B元素的个数为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
6.已知△OAB的直观图△O′A′B′(如图)O′A′=1,∠B′=30°,则△OAB的面积为( )
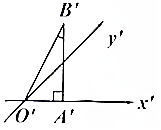

| A. | $\sqrt{6}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\sqrt{3}$ |
 如图,矩形ABCD的边AB=4,AD=2,PA⊥平面ABCD,PA=3,点E在CD上,若PE⊥BE,则PE=$\sqrt{17}$.
如图,矩形ABCD的边AB=4,AD=2,PA⊥平面ABCD,PA=3,点E在CD上,若PE⊥BE,则PE=$\sqrt{17}$.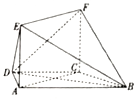 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形.