题目内容
7.已知函数f(x)=$\frac{{{e^x}-{e^{-x}}}}{{{e^x}+{e^{-x}}}}$.(Ⅰ)证明:f(x)为奇函数;
(Ⅱ)判断f(x)单调性并证明;
(III)不等式f(x-t)+f(x2-t2)≥0对于x∈[1,2]恒成立,求实数t的取值范围.
分析 (Ⅰ)根据题意,先分析函数f(x)的定义域,进而可得$f(-x)=\frac{{{e^{-x}}-{e^x}}}{{{e^{-x}}+{e^x}}}=-\frac{{{e^x}-{e^{-x}}}}{{{e^x}+{e^{-x}}}}=-f(x)$,即证明函数为奇函数;
(Ⅱ)先将函数的解析式变形可得$f(x)=\frac{{{e^{2x}}-1}}{{{e^{2x}}+1}}=1-\frac{2}{{{e^{2x}}+1}}$,利用定义法可得证明;
(Ⅲ)根据题意,结合函数的奇偶性与单调性分析,原问题可以转化为当x∈[1,2]时,x2+x≥t2+t恒成立,由二次函数的性质分析可得(x2+x)min=2,进而可得x2+x≥t2+t恒成立?t2+t≤2,解可得t的取值范围,即可得答案.
解答 解:(Ⅰ)证明:对于函数f(x)=$\frac{{{e^x}-{e^{-x}}}}{{{e^x}+{e^{-x}}}}$,其定义域为R,关于原点对称,
∵$f(-x)=\frac{{{e^{-x}}-{e^x}}}{{{e^{-x}}+{e^x}}}=-\frac{{{e^x}-{e^{-x}}}}{{{e^x}+{e^{-x}}}}=-f(x)$,
∴f(x)为奇函数.
( II)f(x)在R上为增函数.
证明:根据题意,$f(x)=\frac{{{e^{2x}}-1}}{{{e^{2x}}+1}}=1-\frac{2}{{{e^{2x}}+1}}$,
在R内任取x1,x2,△x=x2-x1>0,
则$△y=f({x_2})-f({x_1})=({1-\frac{2}{{{e^{2{x_2}}}+1}}})-({1-\frac{2}{{{e^{2{x_1}}}+1}}})=\frac{{2({{e^{2{x_2}}}-{e^{2{x_1}}}})}}{{({{e^{2{x_1}}}+1})({{e^{2{x_2}}}+1})}}$,
∵x2>x1∴2x2>2x1
∴${e^{2{x_2}}}>{e^{2{x_1}}}$,∵${e^{2{x_2}}}\;+1>0\;\;\;\;{e^{2{x_1}}}+1>0$,
∴△y>0.
∴f(x)在R上为增函数.
( III)根据题意,f(x-t)+f(x2-t2)≥0?f(x-t)≥-f(x2-t2),
又由f(x)为奇函数,
∵f(x-t)≥-f(x2-t2)=f(t2-x2),
又∵f(x)在R上为增函数,
∴当x∈[1,2]时,x-t≥t2-x2恒成立,即x2+x≥t2+t恒成立,
而x∈[1,2]时,(x2+x)min=2,
则x2+x≥t2+t恒成立?t2+t≤2,
解得-2≤t≤1,
即t的取值范围是[-2,1].
点评 本题考查函数的恒成立问题,涉及函数的奇偶性、单调性的判定,关键是把恒成立问题转化为最值问题.

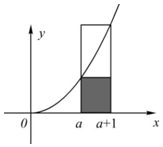 如图所示,由直线x=a,x=a+1(a>0),y=x2及 x 轴围成的曲边梯形的面积介于相应小矩形与大矩形的面积之间,即 a2<$\int_a^{a+1}{\;}$x2dx<(a+1)2.类比之,若对?n∈N*,不等式$\frac{1}{n+1}+\frac{1}{n+2}+…+\frac{1}{2n}$<A<$\frac{1}{n}$+$\frac{1}{n+1}$+…+$\frac{1}{2n-1}$恒成立,则实数A等于( )
如图所示,由直线x=a,x=a+1(a>0),y=x2及 x 轴围成的曲边梯形的面积介于相应小矩形与大矩形的面积之间,即 a2<$\int_a^{a+1}{\;}$x2dx<(a+1)2.类比之,若对?n∈N*,不等式$\frac{1}{n+1}+\frac{1}{n+2}+…+\frac{1}{2n}$<A<$\frac{1}{n}$+$\frac{1}{n+1}$+…+$\frac{1}{2n-1}$恒成立,则实数A等于( )| A. | ln$\frac{5}{2}$ | B. | ln 2 | C. | $\frac{1}{2}$ln 2 | D. | $\frac{1}{2}$ln 5 |
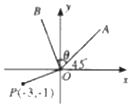 如图,已知点P(-3,-1),OA为第一象限的角平分线,将OA沿逆时针旋转θ角到OB,若$\overrightarrow{OP}•\overrightarrow{OB}=0$,则tanθ的值为( )
如图,已知点P(-3,-1),OA为第一象限的角平分线,将OA沿逆时针旋转θ角到OB,若$\overrightarrow{OP}•\overrightarrow{OB}=0$,则tanθ的值为( )| A. | 2 | B. | 3 | C. | -2 | D. | -3 |
| A. | $-\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $-\frac{1}{3}$ | D. | $\frac{1}{3}$ |
| A. | f2(f(0))=f(f2(0))?? | B. | f2(f(1))=f(f2(1))?? | C. | f2(f(2))=f(f2(2))?? | D. | f2(f(3))=f(f2(3))?? |