题目内容
在△ABC中,D为AC的中点,
(1)若O是中线BD上的一个动点,且 ,求
,求 的最小值;
的最小值;
(2)若O是△ABC的外心,且 ,求
,求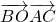 的值.
的值.
解:(1) =
= ((2分) )
((2分) )
 (4分)
(4分)
= (当且仅当
(当且仅当 时取等) (6分)
时取等) (6分)
(2)由O为三角形的外心可得DO⊥AC
 =
= (8分)
(8分)
= (10分)
(10分)
=
= (12分)
(12分)
分析:(1)由 =
= ,利用基本不等式可求最小值
,利用基本不等式可求最小值
(2)由O为三角形的外心可得DO⊥AC,从而可得 =
= =
= ,代入可求
,代入可求
点评:本题主要考查了平面向量的基本数量积的基本运算及利用基本不等式求解最值,平面向量的数量积的性质的应用,属于向量知识的综合应用.
 =
= ((2分) )
((2分) ) (4分)
(4分)=
 (当且仅当
(当且仅当 时取等) (6分)
时取等) (6分)(2)由O为三角形的外心可得DO⊥AC
 =
= (8分)
(8分)=
 (10分)
(10分)=

=
 (12分)
(12分)分析:(1)由
 =
= ,利用基本不等式可求最小值
,利用基本不等式可求最小值(2)由O为三角形的外心可得DO⊥AC,从而可得
 =
= =
= ,代入可求
,代入可求点评:本题主要考查了平面向量的基本数量积的基本运算及利用基本不等式求解最值,平面向量的数量积的性质的应用,属于向量知识的综合应用.

练习册系列答案
相关题目
在△ABC中,D为AB上一点,M为△ABC内一点,且满足
=
,
=
+
,则△AMD与△ABC的面积比为( )
| AD |
| 3 |
| 4 |
| AB |
| AM |
| AD |
| 3 |
| 5 |
| BC |
A、
| ||
B、
| ||
C、
| ||
D、
|
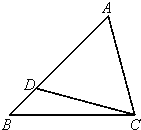 如图,在△ABC中,D为边AB上一点,DA=DC.已知B=
如图,在△ABC中,D为边AB上一点,DA=DC.已知B=