题目内容
在△ABC中，D为BC边的中点，AD=1，点P在线段AD上，则
•(
+
)的最小值为（ ）
| PA |
| PB |
| PC |
分析：设出|AP|，利用D为BC边的中点，AD=1，表示出
+
，然后通过数量积求出表达式的最小值．
| PB |
| PC |
解答：解：在△ABC中，D为BC边的中点，AD=1，点P在线段AD上，
设|AP|=t，t∈（0，1），
则|PD|=1-t，
+
=2
，
•(
+
)=2|
|•|
|cosπ=-2t（1-t）=2t2-2t=2（t-
）2-
，
因为t∈（0，1），
所以2（t-
）2-
的最小值为-
．
•(
+
)的最小值为-
．
故选D．
设|AP|=t，t∈（0，1），
则|PD|=1-t，
| PB |
| PC |
| PD |
| PA |
| PB |
| PC |
| PA |
| PD |
| 1 |
| 2 |
| 1 |
| 2 |
因为t∈（0，1），
所以2（t-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| PA |
| PB |
| PC |
| 1 |
| 2 |
故选D．
点评：本题考查向量在几何中的应用，向量的数量积的应用，考查计算能力，利用几何图形关系表示
+
是解题的关键．
| PB |
| PC |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在△ABC中，D为BC的中点，已知
=
，
=
，则下列向量一定与
同向的是（ ）
| AB |
| a |
| AC |
| b |
| AD |
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
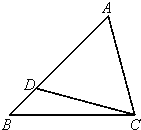如图，在△ABC中，D为边AB上一点，DA=DC．已知B=