题目内容
15.已知集合A={x∈R|x<$\frac{π}{2}$},B={1,2,3,4},则(∁RA)∩B={2,3,4}.分析 先求出(∁UA),再根据交集的运算法则计算即可
解答 解:∵集合A={x∈R|x<$\frac{π}{2}$},
∴(∁UA)={x∈R|x≥$\frac{π}{2}$},
∵B={1,2,3,4},
∴(∁UA)∩B={2,3,4}
故答案为:{2,3,4}.
点评 本题考查集合的交并补运算,属于基础题

练习册系列答案
相关题目
5.若直线x-y-m=0被圆x2+y2-8x+12=0所截得的弦长为$2\sqrt{2}$,则实数m的值为( )
| A. | 2或6 | B. | 0或8 | C. | 2或0 | D. | 6或8 |
3.若角α的顶点为坐标原点,始边与x轴的非负半轴重合,且终边上一点的坐标为(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),则tanα的值为( )
| A. | -$\sqrt{3}$ | B. | -$\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{1}{2}$ |
5.从集合{1,2,3,4,5,6}中随机抽取一个数a,从集合{1,2,3}中随机收取一个数b,则loga2b=1的概率为( )
| A. | $\frac{1}{9}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
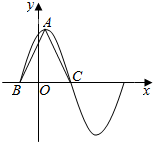 函数f(x)=2$\sqrt{3}$sin(ωx+$\frac{π}{3}$)(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.
函数f(x)=2$\sqrt{3}$sin(ωx+$\frac{π}{3}$)(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.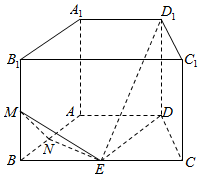 如图,直四棱柱ABCD-A1B1C1D1的底面是等腰梯形,AB=CD=AD=1,BC=2,E,M,N分别是所在棱的中点.
如图,直四棱柱ABCD-A1B1C1D1的底面是等腰梯形,AB=CD=AD=1,BC=2,E,M,N分别是所在棱的中点.