题目内容
4.函数f(x)=x+$\frac{lnx}{x}$在x=1处的切线与两坐标轴围成的三角形的面积为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{2}$ | D. | $\frac{5}{4}$ |
分析 依题意,可得f(1)=1,f'(1)=2,从而可得所求的切线方程为y-1=2(x-1),继而可得它与两坐标轴围成的三角形的面积.
解答 解:$f(x)=x+\frac{lnx}{x}$,
则$f'(x)=1+\frac{{{l}-lnx}}{x^2}$,
因此f(1)=1,f'(1)=2,
故切线方程为y-1=2(x-1).
令x=0,可得y=-1;令y=0,可得$x=\frac{1}{2}$.
故切线与两坐标围成的三角形面积为$\frac{1}{2}×1×\frac{1}{2}=\frac{1}{4}$.
故选:B.
点评 本题考查利用导数研究曲线上某点的切线方程,考查三角形面积的计算,求得函数f(x)=x+$\frac{lnx}{x}$在x=1处的切线方程是关键,属于中档题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
19.在空间直角坐标系O-xyz中,四面体S-ABC各顶点坐标分别是S(1,1,2),A(3,3,2),B(3,3,0),C(1,3,2),则该四面体外接球的表面积是( )
| A. | 16π | B. | 12π | C. | 4$\sqrt{3}$π | D. | 6π |
16.已知集合A={x∈Z|-1<x<3},B={x∈R|x2+x-6<0},则A∩B=( )
| A. | {x|-1<x<2} | B. | {x|-3<x<3} | C. | {0,1} | D. | {0,1,2} |
13.数列{an}通项an=2-($\frac{x+3}{x}$)n,若$\underset{lim}{n→∞}$an=2,则x的取值范围是( )
| A. | (0,-$\frac{3}{2}$] | B. | (0,-$\frac{3}{2}$) | C. | (-∞,-$\frac{3}{2}$) | D. | (-∞,-$\frac{3}{2}$] |
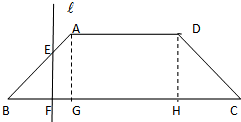 已知底角为45°的等腰梯形ABCD,底边BC长为7cm,腰长为2$\sqrt{2}$cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y与x的函数解析式,并画出大致图象.
已知底角为45°的等腰梯形ABCD,底边BC长为7cm,腰长为2$\sqrt{2}$cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y与x的函数解析式,并画出大致图象.