题目内容
11.已知集合A={x|x2-3x+2≥0},B={x|x≥t}.若A∪B=A,则实数t的取值范围为[2,+∞).分析 集合A={x|x2-3x+2≥0}=(-∞,1]∪[2,+∞),由A∪B=A,可得B⊆A,即可得出.
解答 解:集合A={x|x2-3x+2≥0}=(-∞,1]∪[2,+∞),
B={x|x≥t}.
∵A∪B=A,
∴B⊆A,
∴t≥2.
则实数t的取值范围是[2,+∞).
故答案为:[2,+∞).
点评 本题考查了一元二次不等式的解法、集合之间的关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.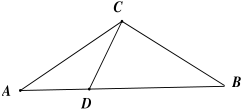 如图,在等腰△ABC中,∠C=120°,DA=DC,过顶点C在∠ACB内部作一条射线CM,与线段AB交于点M,则AM<$\frac{{\sqrt{3}}}{3}$AC的概率为( )
如图,在等腰△ABC中,∠C=120°,DA=DC,过顶点C在∠ACB内部作一条射线CM,与线段AB交于点M,则AM<$\frac{{\sqrt{3}}}{3}$AC的概率为( )
 如图,在等腰△ABC中,∠C=120°,DA=DC,过顶点C在∠ACB内部作一条射线CM,与线段AB交于点M,则AM<$\frac{{\sqrt{3}}}{3}$AC的概率为( )
如图,在等腰△ABC中,∠C=120°,DA=DC,过顶点C在∠ACB内部作一条射线CM,与线段AB交于点M,则AM<$\frac{{\sqrt{3}}}{3}$AC的概率为( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{1}{4}$ |
16.不等式x(1-3x)>0的解集是( )
| A. | (-∞,$\frac{1}{3}$) | B. | (-∞,0)∪(0,$\frac{1}{3}$) | C. | ($\frac{1}{3}$,+∞) | D. | (0,$\frac{1}{3}$) |