题目内容
3.设等比数列{an}的首项a1=1,且4a1,2a2,a3成等差数列,则数列{an}的前10项和S10=1023.分析 设等比数列{an}的公比为q,由题意4q=4+q2,求出q,由此能求出数列{an}的前10项和S10.
解答 解:∵等比数列{an}的首项a1=1,且4a1,2a2,a3成等差数列,
设等比数列{an}的公比为q,
∴4,2q,q2成等差数列,
∴4q=4+q2,解得q=2,
∴数列{an}的前10项和S10=$\frac{1-{2}^{10}}{1-2}$=210-1=1023.
故答案为:1023.
点评 本题考查等比数列的前10项和的求法,是中档题,解题时要认真审题,注意等差数列、等比数列的性质的合理运用.

练习册系列答案
相关题目
13.计算${∫}_{1}^{2}$(x+$\frac{1}{x}$)dx的值为( )
| A. | $\frac{3}{4}$ | B. | $\frac{3}{2}$+ln2 | C. | $\frac{5}{2}$+ln2 | D. | 3+ln2 |
14.设$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$是非零向量,则下列说法中正确的是( )
| A. | ($\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{c}$=($\overrightarrow{c}$-$\overrightarrow{b}$)•$\overrightarrow{a}$ | B. | |$\overrightarrow{a}$-$\overrightarrow{b}$|≤|$\overrightarrow{a}$+$\overrightarrow{b}$| | C. | 若$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$•$\overrightarrow{c}$,则$\overrightarrow{b}$=$\overrightarrow{c}$ | D. | 若$\overrightarrow{a}$∥$\overrightarrow{b}$,$\overrightarrow{a}$∥$\overrightarrow{c}$,则$\overrightarrow{b}$∥$\overrightarrow{c}$ |
15.在线性回归模型中,分别选择了4个不同的模型,它们的相关指数R2依次为0.36、0.95、0.74、0.81,其中回归效果最好的模型的相关指数R2为( )
| A. | 0.95 | B. | 0.81 | C. | 0.74 | D. | 0.36 |
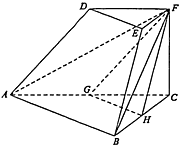 如图,在三棱台DEF-ABC中,已知底面ABC是以AB为斜边的直角三角形,FC⊥底面ABC,AB=2DE,G,H分别为AC,BC的中点.
如图,在三棱台DEF-ABC中,已知底面ABC是以AB为斜边的直角三角形,FC⊥底面ABC,AB=2DE,G,H分别为AC,BC的中点.