题目内容
在平面直角坐标系xOy中,在圆x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足.当点P在圆上运动时,线段PD的中点M的轨迹为C.
(1)求C的参数方程;
(2)直线l的参数方程为
(t为参数),点F(1,-1),已知l与曲线C交于A、B两点,求|AF|+|BF|的值.
(1)求C的参数方程;
(2)直线l的参数方程为
|
考点:参数方程化成普通方程,轨迹方程
专题:坐标系和参数方程
分析:(1)设C(x,y),则P(x,2y),代入圆P所在的方程可得:x2+4y2=4,化为
+y2=1,取x=2cosθ,y=sinθ,即可得出曲线C的参数方程.
(2)把直线l的参数方程
(t为参数),代入曲线C的参数方程可得5t2-6
t+2=0,利用|AF|+|BF|=t1+t2即可得出.
| x2 |
| 4 |
(2)把直线l的参数方程
|
| 2 |
解答:
解:(1)设C(x,y),则P(x,2y),代入圆P所在的方程可得:x2+4y2=4,
化为
+y2=1,取x=2cosθ,y=sinθ,
可得C的参数方程:
,θ为参数.
(2)把直线l的参数方程
(t为参数),代入曲线C的参数方程可得:(1+
t)2+4(-1+
t)2=4,
化为5t2-6
t+2=0,
∴|AF|+|BF|=t1+t2=
.
化为
| x2 |
| 4 |
可得C的参数方程:
|
(2)把直线l的参数方程
|
| ||
| 2 |
| ||
| 2 |
化为5t2-6
| 2 |
∴|AF|+|BF|=t1+t2=
6
| ||
| 5 |
点评:本题考查了曲线的参数方程、中档坐标公式、参数的几何意义,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
设Sn是等差数列{an}的前n项和,若
=
,则
=( )
| a5 |
| a3 |
| 5 |
| 9 |
| S9 |
| S5 |
| A、1 | ||
| B、-1 | ||
| C、2 | ||
D、
|
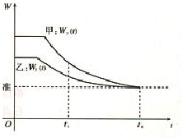 国家环保总局对长期超标准排放污物,污染严重而又未进行治理的单位,规定出一定期限,强令在此期限内完成排污治理.如图是国家环保总局在规定的排污达标日期前,对甲、乙两家企业连续检测的结果(W表示排污量),哪个企业治理的效率比较高?为什么?
国家环保总局对长期超标准排放污物,污染严重而又未进行治理的单位,规定出一定期限,强令在此期限内完成排污治理.如图是国家环保总局在规定的排污达标日期前,对甲、乙两家企业连续检测的结果(W表示排污量),哪个企业治理的效率比较高?为什么?