题目内容
已知等比数列{an}前n项的积为Tn，且公比q≠1，若T7=128，则（ ）
| A、a4=2 |
| B、a5=2 |
| C、a6=2 |
| D、a1=2 |
考点：等比数列的前n项和
专题：等差数列与等比数列
分析：首先利用题中的条件进一步利用性质：在等比数列中，若m+n=p+q，则：am+an=ap+aq，进一步通过运算求出结果．
解答：
解：已知等比数列{an}前n项的积为Tn，且公比q≠1，若T7=128
a1a2a3a4 a5a6 a7=128
利用等比数列的性质：a1a2a3a4 a5a6 a7=a47
所以：a4=2
故选：A
a1a2a3a4 a5a6 a7=128
利用等比数列的性质：a1a2a3a4 a5a6 a7=a47
所以：a4=2
故选：A
点评：本题考查的知识要点：等比数列的性质的应用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
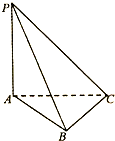如图，在三棱锥P-ABC中，已知△ABC是等腰直角三角形，∠ABC=90°，△PAC是直角三角形，∠PAC=90°，∠ACP=30°，平面PAC⊥平面ABC．不等式||x|-1|≤2的解集为（ ）
| A、[-3，3] |
| B、[-1，3] |
| C、[-3，1] |
| D、[-1，1] |