题目内容
18.已知f(x)=sinx-x,命题p:?x∈(0,$\frac{π}{2}}$),f(x)<0,则( )| A. | p是假命题,¬p::?x∈(0,$\frac{π}{2}}$),f(x)≥0 | B. | p是假命题,¬p::?x∈(0,$\frac{π}{2}}$),f(x)≥0 | ||
| C. | P是真命题,¬p::?x∈(0,$\frac{π}{2}}$),f(x)≥0 | D. | p是真命题,¬p::?x∈(0,$\frac{π}{2}}$),f(x)≥0 |
分析 直接利用特称命题 否定是全称命题写出结果.
解答 解:f(x)=sinx-x,x∈(0,$\frac{π}{2}$),f′(x)=cosx-1<0,∴f(x)是(0,$\frac{π}{2}$)上是减函数,
∵f(0)=0,
∴f(x)<0,
∴命题p:?x∈(0,$\frac{π}{2}$),f(x)<0是真命题,
¬p:?x∈(0,$\frac{π}{2}$),f(x)≥0,
故选:C.
点评 本题考查命题的否定,特称命题与全称命题的否定关系,基本知识的考查.

练习册系列答案
相关题目
8.若函数f(x)=$\frac{{a{x^2}}}{2}-({1+2a})x+2lnx({a>0})$在区间$({\frac{1}{2},1})$内有极大值,则a的取值范围是( )
| A. | $({\frac{1}{e},+∞})$ | B. | (1,+∞) | C. | (1,2) | D. | (2,+∞) |
9.已知等边三角形的一个顶点位于原点,另外两个顶点在抛物线y2=2$\sqrt{3}$x上,则这个等边三角形的边长为( )
| A. | 6$\sqrt{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | 6 | D. | 12 |
6.执行如图所示的程序框图,输出的n的值为( )
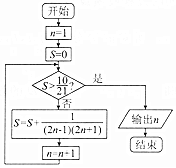

| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
3.已知函数f(x)=$\left\{\begin{array}{l}{lnx,x≥1}\\{1-\frac{x}{2},x<1}\end{array}$,若F(x)=f[f(x)+1]+m有两个零点x1,x2,则x1•x2的取值范围是( )
| A. | [4-2ln2,+∞) | B. | ($\sqrt{e}$,+∞) | C. | (-∞,4-2ln2] | D. | (-∞,$\sqrt{e}$) |
19.连续两次抛掷一枚骰子,记录向上的点数,则向上的点数之差的绝对值为2的概率是( )
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{3}$ |