题目内容
1.中国古代数学名著《九章算术》中记载:今有大夫、不更、簪襃、上造、公士凡五人,共猜得五鹿,欲以爵次分之,问各得几何?意思是:今有大夫、不更、簪襃、上造、公士凡五人,他们共猎获5只鹿,欲按其爵级高低依次递减相同的量来分配,问各得多少,若五只鹿的鹿肉共500斤,则不更、簪襃、上造这三人共分得鹿肉斤数为( )| A. | 200 | B. | 300 | C. | $\frac{500}{3}$ | D. | 400 |
分析 由题意可得该数列以公差为d的等差数列,设簪襃得a,则大夫、不更、簪襃、上造、公士凡以此为a-2d,a-d,a,a+d,a+2d,问题得以解决
解答 解:按其爵级高低依次递减相同的量来分配,故该数列以公差为d的等差数列,设簪襃得a,
则大夫、不更、簪襃、上造、公士凡以此为a-2d,a-d,a,a+d,a+2d,
故a-2d+a-d+a+a+d+a+2d=500,
解得a=100
则不更、簪襃、上造可得a-d+a++a+d=3a=300,
故选:B
点评 本题考查了等差数列的在实际问题中的应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.集合A={x|-2≤x≤3},B={x|x<-1},则A∩(∁RB)等于( )
| A. | {x|x>-1} | B. | {x|x≥-1} | C. | {x|-2≤x≤-1} | D. | {x|-1≤x≤3} |
9.已知等边三角形的一个顶点位于原点,另外两个顶点在抛物线y2=2$\sqrt{3}$x上,则这个等边三角形的边长为( )
| A. | 6$\sqrt{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | 6 | D. | 12 |
6.执行如图所示的程序框图,输出的n的值为( )
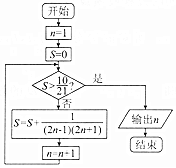

| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
2.若数列{an}满足an+12-an2=d(d为正常数,n∈N*),则称{an}为“等方差数列”.甲:数列{an}是等方差数列;乙:数列{an}是等差数列,则( )
| A. | 甲是乙的充分条件但不是必要条件 | |
| B. | 甲是乙的必要条件但不是充分条件 | |
| C. | 甲是乙的充要条件 | |
| D. | 甲既不是乙的充分条件也不是乙的必要条件 |
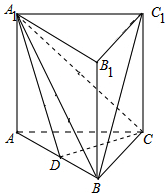 如图,在三棱柱ABC-A1B1C1中,底面△ABC是边长为2的等边三角形,D为AB中点.
如图,在三棱柱ABC-A1B1C1中,底面△ABC是边长为2的等边三角形,D为AB中点.