题目内容
11.已知函数f(x)=|log2|x-1||,且关于x的方程[f(x)]2+af(x)+2b=0有6个不同的实数根,若最小的实数根为-3,则a+b的值为( )| A. | -2 | B. | 4 | C. | 6 | D. | 8 |
分析 先作出函数f(x)=|log2|x-1||的图象,令t=f(x),方程[f(x)]2+af(x)+2b=0转化为:t2+at+2b=0,再方程[f(x)]2+af(x)+2b=0有6个不同的实数解,可知方程t2+at+2b=0有一零根和一正根,又因为最小的实数解为-3,所以f(-3)=2从而得到方程:t2+at+2b=0的两根是0和2,最后由韦达定理求得得:a,b进而求得a+b的值.
解答  解:作出函数f(x)=|log2|x-1||的图象,如图所示:
解:作出函数f(x)=|log2|x-1||的图象,如图所示:
∵方程[f(x)]2+af(x)+2b=0有6个不同的实数解,
令t=f(x),方程[f(x)]2+af(x)+2b=0转化为:t2+at+2b=0,
则关于t的方程有一零根和一正根,
又∵最小的实数解为-3,由f(-1)=2,
∴方程:t2+at+2b=0的两根是0和2,
由韦达定理得:a=-2,b=0,
∴a+b=-2,
故选:A.
点评 本题主要考查函数与方程的综合运用,还考查了方程的根与函数零点的关系,属于中档题.

练习册系列答案
相关题目
4.若A,B,C是函数f(x)=ex+x图象上横坐标成等差数列的三个点,给出以下判断:①△ABC可能是直角三角形;②△ABC一定是钝角三角形;③△ABC可能是等腰三角形;④△ABC一定不是等腰三角形.其中,正确的判断是( )
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
19.在平面直角坐标系xOy中,已知点A(2,0),直线l:x+y-5=0,点B(x,y)是圆C:x2+2x+y2-1=0上的动点,AD⊥l,BE⊥l,垂足分别为D,E,则线段DE的最大值是( )
| A. | $\sqrt{2}$ | B. | $\frac{{3\sqrt{2}}}{2}$ | C. | $2\sqrt{2}$ | D. | $\frac{{5\sqrt{2}}}{2}$ |
3.数列1,3,6,10,15,…的递推公式是( )
| A. | an+1=an+n,n∈N* | B. | an=an-1+n,n∈N*,n≥2 | ||
| C. | an+1=an+(n+1),n∈N*,n≥2 | D. | an=an-1+(n-1),n∈N*,n≥2 |
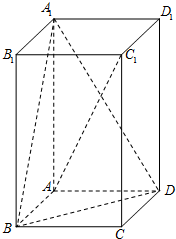 如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=h.
如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=h.