题目内容
1.已知三棱锥A-BCD中,DA⊥平面BCD,底面△BCD为等边三角形,且BC=2,AD=2$\sqrt{3}$,则此三棱锥的外接球的表面积为$\frac{52}{3}$π.分析 由已知结合三棱锥和正三棱柱的几何特征,可得此三棱锥外接球,即为以△BCD为底面以DA为高的正三棱柱的外接球,分别求出棱锥底面半径r,和球心距d,可得球的半径R,即可求出三棱锥A-BCD外接球的表面积.
解答 解:根据已知中底面△BCD是边长为2的正三角形,DA⊥平面BCD,可得此三棱锥外接球,即为以△BCD为底面以DA为高的正三棱柱的外接球
∵△BCD是边长为2的正三角形,
∴△BCD的外接圆半径r=$\frac{2\sqrt{3}}{3}$,
球心到△BCD的外接圆圆心的距离d=$\sqrt{3}$,
故球的半径R=$\sqrt{3+\frac{4}{3}}$=$\sqrt{\frac{13}{3}}$,
故三棱锥P-ABC外接球的表面积S=4πR2=$\frac{52}{3}$π,
故答案为:$\frac{52}{3}$π.
点评 本题考查的知识点是球内接多面体,正确求出球的半径R是解答的关键.

练习册系列答案
相关题目
11.设a<b,函数y=(x-a)2(x-b)的图象可能是( )
| A. |  | B. |  | C. |  | D. | D |
12.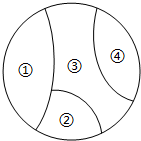 将某城市分成如图所示的4个区,需要绘制一幅城市分区地图,有红、黄、蓝、绿、紫5种不同的颜色,图中①、②、③、④每区只涂一色,且相邻两区必须涂不同颜色,则涂色时恰好用了3种不同颜色的概率是( )
将某城市分成如图所示的4个区,需要绘制一幅城市分区地图,有红、黄、蓝、绿、紫5种不同的颜色,图中①、②、③、④每区只涂一色,且相邻两区必须涂不同颜色,则涂色时恰好用了3种不同颜色的概率是( )
 将某城市分成如图所示的4个区,需要绘制一幅城市分区地图,有红、黄、蓝、绿、紫5种不同的颜色,图中①、②、③、④每区只涂一色,且相邻两区必须涂不同颜色,则涂色时恰好用了3种不同颜色的概率是( )
将某城市分成如图所示的4个区,需要绘制一幅城市分区地图,有红、黄、蓝、绿、紫5种不同的颜色,图中①、②、③、④每区只涂一色,且相邻两区必须涂不同颜色,则涂色时恰好用了3种不同颜色的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{5}$ |
16.函数f(x)=$\frac{2+sinx}{1+{x}^{2}}$是( )
| A. | 奇函数 | B. | 偶函数 | C. | 有界函数 | D. | 周期函数 |