题目内容
16.函数f(x)=$\frac{2+sinx}{1+{x}^{2}}$是( )| A. | 奇函数 | B. | 偶函数 | C. | 有界函数 | D. | 周期函数 |
分析 利用函数的奇偶性和周期性的定义逐一排除A,B,D,则答案可求.
解答 解:函数f(x)=$\frac{2+sinx}{1+{x}^{2}}$的定义域为R,
又f(-x)=$\frac{2+sin(-x)}{1+(-x)^{2}}=\frac{2-sinx}{1+{x}^{2}}$≠f(x),
且f(-x)≠-f(x),
∴f(x)为非奇非偶的函数,排除A,B;
又f(x+2kπ)=$\frac{2+sin(x+2kπ)}{1+(x+2kπ)^{2}}=\frac{2+sinx}{1+(x+2kπ)^{2}}$≠$\frac{2+sinx}{1+{x}^{2}}$(k∈Z且k≠0),
∴f(x)不是周期函数,排除D;
故选:C.
点评 本题考查函数的奇偶性,周期性的判断,是中档题.

练习册系列答案
相关题目
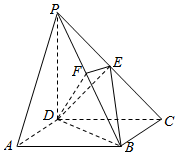 如图,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F.