题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c,已知a+b=8,c=7,
•
=-
.
(1)求角C;
(2)若sin(α+C)=
(0<α<π),求sinα的值.
| CA |
| CB |
| 15 |
| 2 |
(1)求角C;
(2)若sin(α+C)=
| 1 |
| 3 |
考点:平面向量数量积的运算,两角和与差的正弦函数
专题:平面向量及应用
分析:(1)△ABC中,由
•
=-
,c=7,结合余弦定理可得a2+b2=34,再由a+b=8,求得ab的值,可得cosC的值,从而求得C.
(2)由条件气的α+
∈(
,π),cos(α+C)=-
,再根据sinα=sin[(α+
)-
]利用两角差的正弦公式求得结果.
| CA |
| CB |
| 15 |
| 2 |
(2)由条件气的α+
| 2π |
| 3 |
| 2π |
| 3 |
2
| ||
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
解答:
解:(1)△ABC中,∵
•
=ab•cosC=-
,c=7,
再由余弦定理可得 c2=49=a2+b2-2ab•cosC=a2+b2+15,∴a2+b2=34,
再由a+b=8,∴ab=15,cosC=-
,C=
.
(2)∵sin(α+C)=
(0<α<π),∴α+
∈(
,
),∴α+
∈(
,π),
cos(α+C)=-
,
∴sinα=sin[(α+
)-
]=sin(α+
)cos
-cos(α+
)sin
=
(-
)-(-
)
=
.
| CA |
| CB |
| 15 |
| 2 |
再由余弦定理可得 c2=49=a2+b2-2ab•cosC=a2+b2+15,∴a2+b2=34,
再由a+b=8,∴ab=15,cosC=-
| 1 |
| 2 |
| 2π |
| 3 |
(2)∵sin(α+C)=
| 1 |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| 5π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
cos(α+C)=-
2
| ||
| 3 |
∴sinα=sin[(α+
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
=
| 1 |
| 3 |
| 1 |
| 2 |
2
| ||
| 3 |
| ||
| 2 |
2
| ||
| 6 |
点评:本题主要考查两个向量的数量积的定义,余弦定理、两角和差的三角公式的应用,属于中档题.

练习册系列答案
相关题目
如图为一个几何体是三视图,则该几何体的表面积(不考虑接触点)为( )

A、6+
| ||
| B、32+π | ||
C、18+
| ||
D、18+2
|
在区间[0,π]内任取一个数x,则使sinx-cosx≤0的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设复数z1=1+i,z2=
-i,其中i为虚数单位,则
的实部为( )
| 3 |
| z1 |
| z2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设a1,a2,a3均为正数,λ1<λ2<λ3,则函数f(x)=
+
+
的两个零点分别位于区间( )
| a1 |
| x-λ1 |
| a2 |
| x-λ2 |
| a3 |
| x-λ3 |
| A、(-∞,λ1)∪(λ1,λ2)内 |
| B、(λ1,λ2)∪(λ2,λ3)内 |
| C、(λ2,λ3)∪(λ3,+∞)内 |
| D、(-∞,λ1)∪(λ3,+∞)内 |
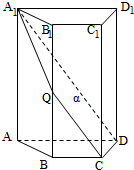 如图,四棱柱ABCD-A1B1C1D1中,A1A⊥底面ABCD,四边形ABCD为梯形,AD∥BC,且AD=2BC,过A1、C、D三点的平面记为α,BB1与α的交点为Q.
如图,四棱柱ABCD-A1B1C1D1中,A1A⊥底面ABCD,四边形ABCD为梯形,AD∥BC,且AD=2BC,过A1、C、D三点的平面记为α,BB1与α的交点为Q.