题目内容
若cosαcosβ+sinαsinβ=0，则sinαcosβ-cosαsinβ值为 ．
考点：两角和与差的正弦函数
专题：三角函数的求值
分析：由cosαcosβ+sinαsinβ=cos（α-β）=0，可得α-β=kπ+
，k∈Z，从而可求sinαcosβ-cosαsinβ=sin（α-β）=1或-1．
| π |
| 2 |
解答：
解：∵cosαcosβ+sinαsinβ=0，
∴cos（α-β）=0，
∴α-β=kπ+
，k∈Z，
∴sinαcosβ-cosαsinβ=sin（α-β）=1或-1．
故答案为：1或-1．
∴cos（α-β）=0，
∴α-β=kπ+
| π |
| 2 |
∴sinαcosβ-cosαsinβ=sin（α-β）=1或-1．
故答案为：1或-1．
点评：本题主要考察了角和与差的正弦函数公式的应用，三角函数的求值，属于基本知识的考查．
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
相关题目
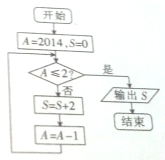如图，该程序框图运行后输出的结果为（ ）| A、4024 | B、4026 |
| C、4028 | D、4020 |
两直线3x+y-
m=0与6x+my+1=0平行，则它们之间的距离为（ ）
| 3 |
| 2 |
| A、4 | ||||
B、
| ||||
C、
| ||||
D、
|
设全集为R，集合A={x|
≥0}，B={x|-2≤x＜0}，则（∁RA）∩B等于（ ）
| x-1 |
| x+1 |
| A、（-1，0） |
| B、[-1，0） |
| C、[-2，-1] |
| D、[-2，-1） |