题目内容
6.直线l将圆x2+y2-2x-4y=0平分,且与直线x+2y=0平行,直线l的方程为( )| A. | 2x-y=0 | B. | 2x-y-2=0 | C. | x+2y-3=0 | D. | x+2y-5=0 |
分析 设出与已知直线平行的直线方程,利用直线平分圆的方程,求出结果即可.
解答 解:设与直线x+2y=0平行的直线方程:x+2y+b=0,
圆C:x2+y2-2x-4y=0化为(x-1)2+(y-2)2=5,圆心坐标(1,2).
因为直线平分圆,圆心在直线x+2y+b=0,所以1+4+b=0,解得b=-5,
故所求直线方程为x+2y-5=0.
故选D.
点评 本题是基础题,考查直线与圆的位置关系,直线与直线平行的方程的设法,考查计算能力.

练习册系列答案
相关题目
14.“a(a-1)≤0”是“方程x2+x-a=0有实数根”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
5.定义域为R的函数f(x)满足f(x+1)=2f(x),且当x∈[0,1]时,f(x)=x2-x,则当x∈[-2,-1]时,f(x)的最小值为( )
| A. | -$\frac{1}{16}$ | B. | -$\frac{1}{8}$ | C. | -$\frac{1}{4}$ | D. | 0 |
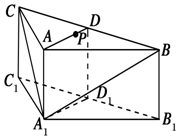 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC,D,D1分别是线段BC,B1C1的中点,P是线段AD上异于端点的点.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC,D,D1分别是线段BC,B1C1的中点,P是线段AD上异于端点的点.