题目内容
18．已知函数f（x）=ax2+bx+4ln x的极值点为1和2．（1）求实数a，b的值；
（2）求函数f（x）在定义域上的极大值、极小值．
分析 （1）求出函数的导数，根据f（x）的极值点，求出a，b的值即可；
（2）求出函数的导数，解关于导函数的不等式，求出函数的单调区间，从而求出函数的极值即可．
解答 解：f′（x）=2ax+b+$\frac{4}{x}$=$\frac{2{ax}^{2}+bx+4}{x}$，x∈（0，+∞），
（1）∵y=f（x）的极值点为1和2，
∴2ax2+bx+4=0的两根为1和2，
∴$\left\{\begin{array}{l}{1+2=-\frac{b}{2a}}\\{1×2=\frac{4}{2a}}\end{array}\right.$，解得a=1，b=-6．
（2）由（1）得：f（x）=x2-6x+4lnx，
函数f（x）的定义域是（0，+∞），
f′（x）=$\frac{2（x-1）（x-2）}{x}$，
令f′（x）＞0，解得：x＞2或0＜x＜1，
令f′（x）＜0，解得：1＜x＜2，
故f（x）在（0，1）递增，在（1，2）递减，在（2，+∞）递增，
故f（x）极大值=f（1）=-5，f（x）极小值=f（2）=-8+4ln2．
点评 本题考查了函数的单调性、极值问题，考查导数的应用，是一道中档题．
练习册系列答案
相关题目
8．在△ABC中，角A，B，C的对边分别为a，b，c，∠A，∠B，∠C的大小成等差数列，且a=1，$b=\sqrt{3}$．则∠A的大小为（ ）
| A． | $\frac{π}{6}$或$\frac{5π}{6}$ | B． | $\frac{π}{3}$或$\frac{2π}{3}$ | C． | $\frac{π}{6}$ | D． | $\frac{π}{3}$ |
6．直线l将圆x2+y2-2x-4y=0平分，且与直线x+2y=0平行，直线l的方程为（ ）
| A． | 2x-y=0 | B． | 2x-y-2=0 | C． | x+2y-3=0 | D． | x+2y-5=0 |
13．求曲线y=x2与y2=x所围成封闭图形的面积，其中正确的是（ ）
| A． | S=${∫}_{0}^{1}$（$\sqrt{x}$-x2）dx | B． | S=${∫}_{0}^{1}$（y2-$\sqrt{x}$）dx | C． | S=${∫}_{0}^{1}$（x2-$\sqrt{x}$）dx | D． | S=${∫}_{0}^{2}$（$\sqrt{y}$-y2）dy |
10．
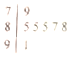在华中师大一附中首届数学节的演讲比赛中，七位评委为某参赛教师打出的分数的茎叶图如图所示，去掉最高分和最低分后，这位老师得分的方差为（ ）
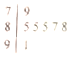在华中师大一附中首届数学节的演讲比赛中，七位评委为某参赛教师打出的分数的茎叶图如图所示，去掉最高分和最低分后，这位老师得分的方差为（ ）| A． | 1.14 | B． | 1.6 | C． | 2.56 | D． | 3 |