题目内容
14.“a(a-1)≤0”是“方程x2+x-a=0有实数根”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 方程x2+x-a=0有实数根?△=1+4a≥0,解得a范围.a(a-1)≤0解得:0≤a≤1.即可判断出结论.
解答 解:方程x2+x-a=0有实数根?△=1+4a≥0,解得a≥-$\frac{1}{4}$.
a(a-1)≤0解得:0≤a≤1.
∴“a(a-1)≤0”是“方程x2+x-a=0有实数根”的充分不必要条件.
故选:A.
点评 本题考查了不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
2.下列选项错误的是( )
| A. | 命题:“若x≠2,则x2-5x+6≠0”的逆否命题是“若x2-5x+6=0,则x=2” | |
| B. | “x<1”是“x2-3x+2>0”的充分不必要条件 | |
| C. | 若命题“p:?x∈R,x2+x+1≠0”,则“¬p:?x0∈R,x02+x0+1=0” | |
| D. | 若“p∨q”为真命题,则p,q均为真命题 |
19. 某高校共有学生15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
某高校共有学生15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生的样本数据?
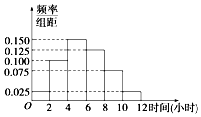
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据的分组区间为:[0,2],(2,4],(4,6],(6,8],(8,10],(10,12]
①估计该校学生每周平均体育运动时间超过4小时的概率P;
②假设该校每个学生每周平均体育运动时间超过4小时的概率都为P,试求从中任选三人至少有一人每周平均体育运动时间超过4小时的概率
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4小时,请完成每周平均体育运动时间与性别列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
附:K2=$\frac{n(ad-bc)2}{(a+b)(c+d)(a+c)(b+d)}$.
 某高校共有学生15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
某高校共有学生15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).(1)应收集多少位女生的样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据的分组区间为:[0,2],(2,4],(4,6],(6,8],(8,10],(10,12]
①估计该校学生每周平均体育运动时间超过4小时的概率P;
②假设该校每个学生每周平均体育运动时间超过4小时的概率都为P,试求从中任选三人至少有一人每周平均体育运动时间超过4小时的概率
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4小时,请完成每周平均体育运动时间与性别列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
| 男生 | 女生 | 总计 | |
| 每周平均体育运动时间不超过4小时 | 45 | 30 | 75 |
| 每周平均体育运动时间超过4小时 | 165 | 60 | 225 |
| 总计 | 210 | 90 | 300 |
6.直线l将圆x2+y2-2x-4y=0平分,且与直线x+2y=0平行,直线l的方程为( )
| A. | 2x-y=0 | B. | 2x-y-2=0 | C. | x+2y-3=0 | D. | x+2y-5=0 |
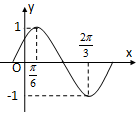 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.