题目内容
17.已知正方形ABCD的边长为2,E为CD的中点,则$\overrightarrow{AE}$•$\overrightarrow{AC}$=6.分析 由题意建立平面直角坐标系,求出向量的坐标,由数量积的坐标运算得答案.
解答 解:建立如图所示的平面直角坐标系,
∵正方形ABCD的边长为2,∴C(2,2),E(1,2),
∴$\overrightarrow{AE}$=(1,2),$\overrightarrow{AC}$=(2,2),
则$\overrightarrow{AE}$•$\overrightarrow{AC}$═(1,2)•(2,2)=2×1+2×2=6.
故答案为:6.
点评 本题考查平面向量的数量积运算,利用坐标法求解,起到事半功倍的效果,属基础题.

练习册系列答案
相关题目
7.已知函数$f(x)=\left\{\begin{array}{l}\frac{2}{x},x≥2\\{(x-1)^3},x<2\end{array}\right.$,若关于x的方程f(x)+k=0有两个不同的实根,则实数k的取值范围是( )
| A. | (0,1) | B. | [0,1] | C. | (-1,0) | D. | [-1,0] |
8.在△ABC中,角A,B,C的对边分别为a,b,c,∠A,∠B,∠C的大小成等差数列,且a=1,$b=\sqrt{3}$.则∠A的大小为( )
| A. | $\frac{π}{6}$或$\frac{5π}{6}$ | B. | $\frac{π}{3}$或$\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{3}$ |
2.下列选项错误的是( )
| A. | 命题:“若x≠2,则x2-5x+6≠0”的逆否命题是“若x2-5x+6=0,则x=2” | |
| B. | “x<1”是“x2-3x+2>0”的充分不必要条件 | |
| C. | 若命题“p:?x∈R,x2+x+1≠0”,则“¬p:?x0∈R,x02+x0+1=0” | |
| D. | 若“p∨q”为真命题,则p,q均为真命题 |
6.直线l将圆x2+y2-2x-4y=0平分,且与直线x+2y=0平行,直线l的方程为( )
| A. | 2x-y=0 | B. | 2x-y-2=0 | C. | x+2y-3=0 | D. | x+2y-5=0 |
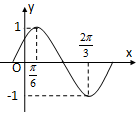 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.