题目内容
已知函数f(x)=
sin(2x+
).
(1)求函数f(x)的最小值及取得最小值时相应的x的取值集合;
(2)求函数f(x)的最小正周期及单调递增区间;
(3)已知△ABC中,角A,B,C所对的边长分别为a,b,c,若f(C)=0,a=
,b=2,求△ABC的面积S.
| ||
| 2 |
| π |
| 3 |
(1)求函数f(x)的最小值及取得最小值时相应的x的取值集合;
(2)求函数f(x)的最小正周期及单调递增区间;
(3)已知△ABC中,角A,B,C所对的边长分别为a,b,c,若f(C)=0,a=
| 3 |
考点:正弦函数的单调性,三角形的面积公式
专题:三角函数的图像与性质,解三角形
分析:(1)首先可以根据函数的解析式f(x)=
sin(2x+
)直接利用函数相应的性质,求得函数f(x)的最小值及取得最小值时相应的x的取值集合,
(2)同样可以利用具体的性质求得函数的最小正周期和单调递增区间.
(3)利用(1)函数f(x)=
sin(2x+
)先求的C的大小,然后利用三角形的面积公式求的结果.
| ||
| 2 |
| π |
| 3 |
(2)同样可以利用具体的性质求得函数的最小正周期和单调递增区间.
(3)利用(1)函数f(x)=
| ||
| 2 |
| π |
| 3 |
解答:
解:(1)已知函数f(x)=
sin(2x+
) 则:f(x)的最小值为-
此时2x+
=2kπ-
(k∈Z)解得:x=kπ-
(k∈Z)
所以相应的x的取值集合为:{x|x=x=kπ-
(k∈Z)}
(2)根据正弦型函数的最小正周期公式:
T=
=π
利用整体思想函数的单调递增区间:
2kπ-
≤2x+
≤2kπ+
(k∈Z)
解得:kπ-
≤x≤kπ+
(k∈Z)
所以函数的单调递增区间为[kπ-
,kπ+
](k∈Z)
(3)由题意知f(C)=0
∴
sin(2C+
)=0
∴sin(2C+
)=0
∵C为三角形的内角
∴0<C<π
则
<2C+
<2π+
解得:C=
或C=
由于a=
,b=2
①当C=
时,根据三角巷的面积公式:
S△=
absinC=
②当C=
时,根据三角巷的面积公式:
S△=
absinC=
| ||
| 2 |
| π |
| 3 |
| ||
| 2 |
此时2x+
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
所以相应的x的取值集合为:{x|x=x=kπ-
| 5π |
| 12 |
(2)根据正弦型函数的最小正周期公式:
T=
| 2π |
| 2 |
利用整体思想函数的单调递增区间:
2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
解得:kπ-
| 5π |
| 12 |
| π |
| 12 |
所以函数的单调递增区间为[kπ-
| 5π |
| 12 |
| π |
| 12 |
(3)由题意知f(C)=0
∴
| ||
| 2 |
| π |
| 3 |
∴sin(2C+
| π |
| 3 |
∵C为三角形的内角
∴0<C<π
则
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
解得:C=
| π |
| 3 |
| 5π |
| 6 |
由于a=
| 3 |
①当C=
| π |
| 3 |
S△=
| 1 |
| 2 |
| 3 |
| 2 |
②当C=
| 5π |
| 6 |
S△=
| 1 |
| 2 |
| ||
| 2 |
点评:本题考查的知识点:正弦型三角函数函数的最值,最小正周期,单调递增区间,以及解三角形的面积公式,要准确加以记忆.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
若函数f(x)=loga(x+b)(a>0,a≠1)的图象经过点(-1,0)和(0,1),则该函数的反函数是( )
| A、y=2x+2 |
| B、y=2x+1 |
| C、y=2x-2 |
| D、y=2x-1 |
在等差数列{an}中,a1=3,a3=6则a5的值为( )
| A、15 | B、6 | C、81 | D、9 |
 随机抽取某中学甲乙两个班各10名同学,测得他们的身高(单位:cm)获得身高数据的茎叶图,如图所示:
随机抽取某中学甲乙两个班各10名同学,测得他们的身高(单位:cm)获得身高数据的茎叶图,如图所示: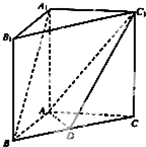 如图,在直三棱柱ABC-A1B1C1中,点D是BC的中点.
如图,在直三棱柱ABC-A1B1C1中,点D是BC的中点.