题目内容
19.设向量$\overrightarrow{a}$、$\overrightarrow{b}$满足:|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,$\overrightarrow{a}$•$\overrightarrow{b}$=1,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角是( )| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
分析 利用向量的数量积,通过三角函数的化简求解即可.
解答 解:向量$\overrightarrow{a}$、$\overrightarrow{b}$满足:|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,$\overrightarrow{a}$•$\overrightarrow{b}$=1,
可得$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$||$\overrightarrow{b}$|cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=2cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=1,
可得cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{1}{2}$,
<$\overrightarrow{a}$,$\overrightarrow{b}$>=60°.
故选:B.
点评 本题考查平面向量的数量积的运算,向量的夹角的求法,考查计算能力.

练习册系列答案
相关题目
9.某人从甲地去乙地共走了500m,途经一条宽为x m的河流,该人不小心把一件物品丢在途中,若物品掉在河里就找不到,若物品不掉在河里就能找到.已知该物品能被找到的概率为$\frac{24}{25}$,则河宽为( )
| A. | 80m | B. | 20m | C. | 40m | D. | 50m |
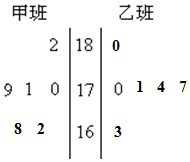 随机抽取某中学甲乙两班各6名学生,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.
随机抽取某中学甲乙两班各6名学生,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.